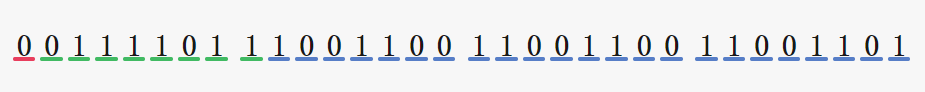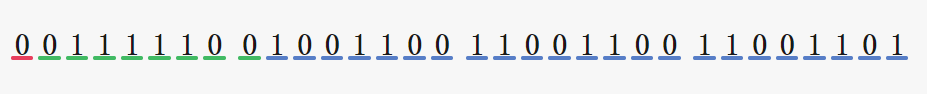万字长文揭开浮点数的所有秘密

05 定点数和浮点数

你会如何存储实数

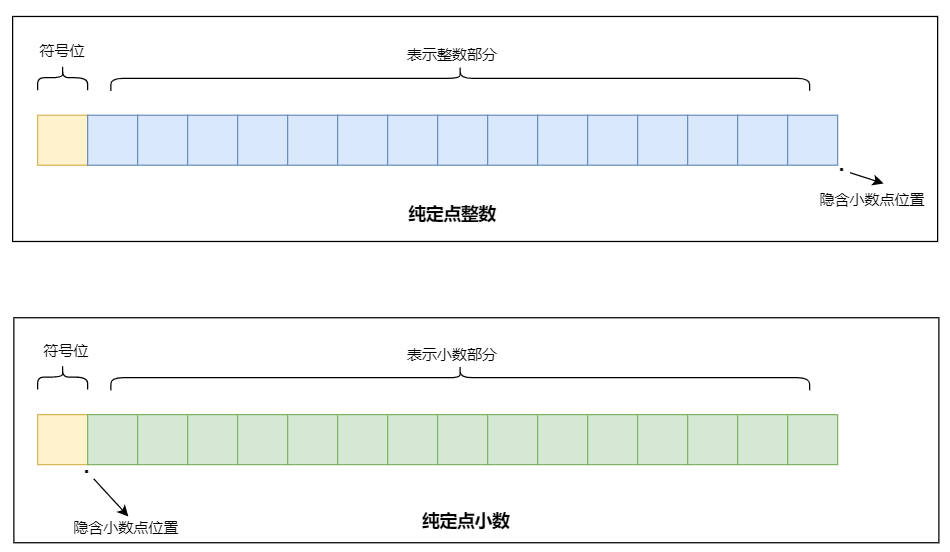
计算机的存储位宽是固定的，比如说固定 16 位，如何用这 16 位来储存带符号且既有整数部分又有小数部分的实数呢？

你可以这样：

用来分开整数和小数部分的小数点甚至可以不存储，只要知道这两部分在哪分开就行了，可以把这个空位让给整数部分或小数部分，纯凭个人喜好，那就让给整数部分吧，这样整数部分能表示的数值范围更大一些，然后变成这样：

符号位部分我们可以采用和原码一样的表示方式，1 代表负数，0 代表正数。整数部分占 8 位，可以存 0 到 255 的整数。小数部分占 7 位，可以存 0.0 到 0.9921875[^1] 的小数。

我们把 -253.25 存到进去看看：

然后又把 -1.9921875 存进去看看：

发现问题

固定整数和小数的储存位宽之后，你有没有发现一个问题：

当你想存一个整数部分比较大，小数部分比较短（精度较低）的数的时候，比如 258.125，发现存不下了，整数部分最大能存255，可是小数部分还有很多空位。

当你想存整数部分比较小，小数部分比较长（精度较高）的数的时候，比如 1.1545845875458454，发现也存不了[^3]。

整数部分用越多存储空间能表示的实数的范围越广，小数部分用越多的存储空间表示的实数的精度越高。

这种小数点的位置固定不变的实数的储存方式叫定点数，它的缺点就是有可能会造成空间的浪费。

要是小数点能根据需求自由移动就好了：存精度高的数的时候小数部分就多占一点位置，存数值大的数的时候整数部分就多占一点位置。

科学记数法

如何才能自由的移动小数点呢？让我们先来回忆下科学记数法：

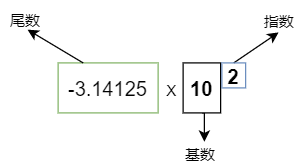
-314.125 用科学记数法表示为：-3.14125 X 10²

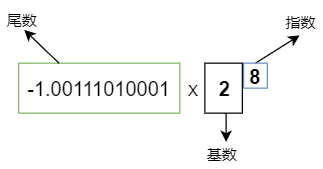
-314.125 转换成二进制得 -100111010.001[^2]， 然后也用科学记数法表示：

发现规律

从十进制和二进制的科学记数法那里发现了一个规律：科学记数法中，我们可以用指数来控制小数点的位置。

比如 -314.125 在十进制中你可以表示成 -3.14125 X 10² ，小数点比原来前移动了 2 位。

它的二进制 -100111010.001 你可以表示成 -1.00111010001 X 2⁸ ，小数点比原来前移动了 8 位。

那我们就可以采用二进制科学记数法来表示实数，把尾数和指数存起来，实数的小数点就能自由移动，这种小数点可以变动的数叫浮点数

IEEE 754 标准

用科学记数法表示实数能让小数点的位置可以移动，但是尾数、指数占几位存储空间或怎么存都没有一个规定，如果各规定各的，比如 JAVA 中规定这样这样，C 语言中又规定那样那样，intel 平台的硬件这样实现，AMD 平台的硬件那样实现，那岂不是乱套了，而且很不方便代码移植。所以有了 IEEE 754 标准（本文以单精度为例，双精度类似）。

存储格式

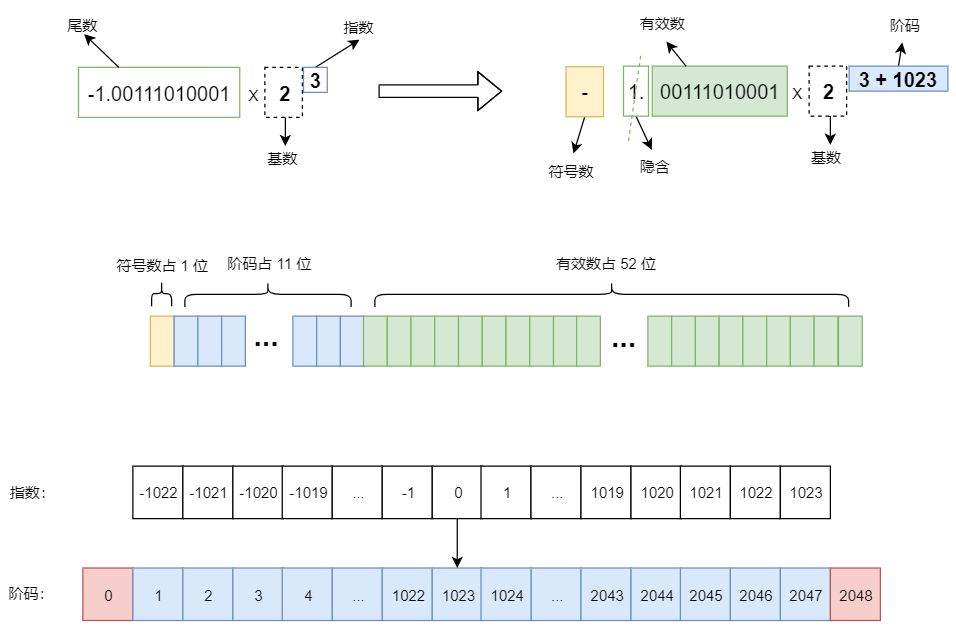
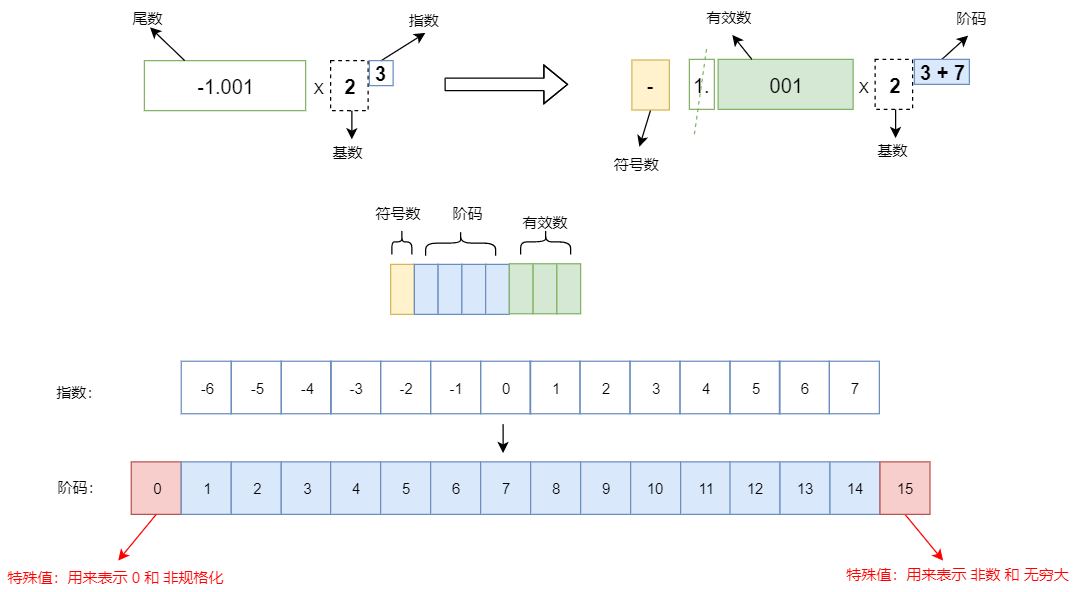
标准规定 32 位单精度浮点数这么存：

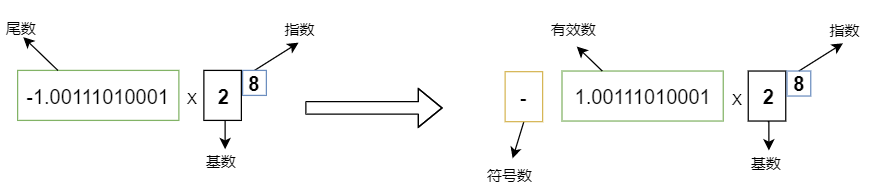
但是你发现，不是存尾数、指数吗？符号数你还能理解，就是用 1 或 0 表示尾数部分的正负号，但是有效数和阶码是个什么东西？

有效数

现在让我们先猜有效数，你可能会这样猜：

很接近了，但是还不对。

十进制科学记数法中，尾数规定其绝对值只能大于等于 1 且小于 10，即尾数绝对值不能大于基数 ，也就是能表示成 ±3.03456 x 10ⁿ 但不能表示成 ±30.3456 x 10ⁿ，因为这样表示，我们无法通过直接比较指数 n 就知道两个实数的大小。

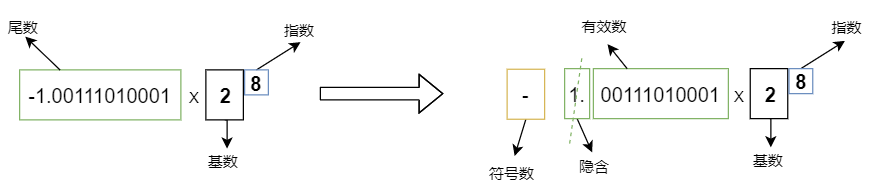
二进制科学记数法也一样，尾数规定其绝对值只能大于等于 1 且小于 2，就只能这样表示 ±1.****** x 2ⁿ ，又由于我们把符号位单独用符号数表示了，剩下的尾数部分一定是以 1. 开头。

既然一定是 1. 开头，那这个 1. 可以不存，这样节省了空间，我们取出来时前面再拼接上 1. 即可得到原来得值。

所以正确的有效数应该是这样：

阶码

阶码呢？

我们的指数不单有正数，还得有负数，比如十进制的 -0.0078125，它的二进制为 -0.0000001，用二进制科学记数法表示为 -1.0 x 2^-7

如何表示负数呢？我们学过原码、反码、补码都可以表示负数，也就是最高位为 1 时表示负数 。

但使用这三种编码有一个问题，就是不方便直接比较指数的大小，从而间接的得到两个实数的大小。因为两个普通二进制数比大小，只要从最高位开始比，两个数的对应位相同则继续往后比，只要不相同，位是 1 的数就一定大于位是 0 的数。使用原码、反码、补码，由于最高位是 1 时表示负数，表示的数反而更小，用这种方式比，负数和正数或负数和负数比大小时，结果会出错。如果非要用这三种编码，既要处理尾数符号位，又要处理指数的符号位，麻烦。

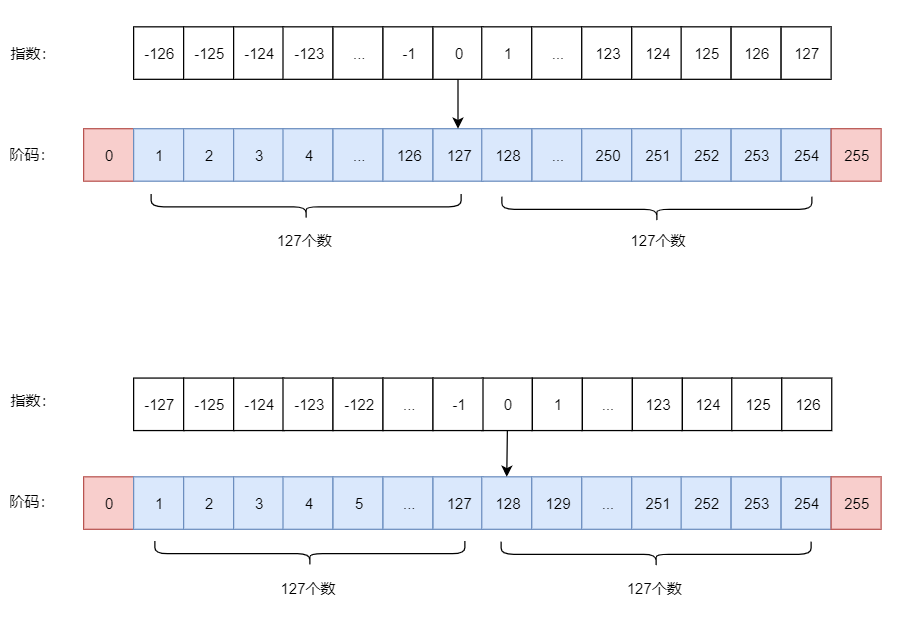
所以我们可以把负数映射成正数，比如 8 位二进制，能表示的范围就是 0~255 共 256 个数：

同时附上一张双精度浮点数的图：

中间数是 127 和 128 选其中一个表示 0 都可以，然后正负数向两边延申。

如果取 127 那么指数表示的范围就是 [-126，127]，如果取128 那么指数的表示范围就是[-127，126]。

也就是取 127 能表示的数范围更广，取 128 能表示的数精度更高，最终 IEEE 754 选择了 127。

所以阶码 = 指数 + 127，阶码通过一个原始值偏移一个值（如这里的127）得到，这种编码方式又叫移码。

用一张图概括上面的知识：

非数、无穷大

我为什么会把阶码 0 和 255 用红色标记呢，当然是有原因的，它们被用来表示特殊用途。

先来思考以下问题，答案我已给出

• -4 的平方根是多少，或者说根号 -4 的结果是什么？

  负数没有平方根，-4 的平方根不是一个数，即非数。

• 高等数学中 1 除以 0 结果是什么？

  无穷大。

• 当两个很大得浮点数相加后结果超出存储范围怎么办？

  IEEE 754 不像补码底层是模运算“不会”超出存储范围，当两个很大的浮点数相加后结果超出存储范围时，会尝试先进行舍入操作返回一个尽可能接近的值，如果进行舍入操作后还是超出存储范围就返回无穷大。

所以，还需要表示两种特殊的数：非数和无穷大

IEEE 754 规定：当阶码为 255 时，如果有效数是 0 那么表示无穷大，有效数是其他任何数则表示非数。

实数零

那阶码 0 的特殊用途呢？

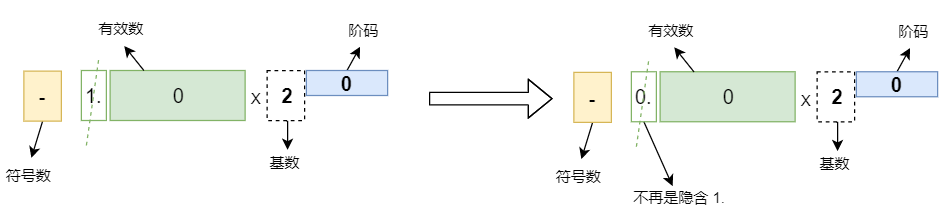
我们看上面那句话：”二进制科学记数法，尾数规定其绝对值只能大于等于 1 且小于 2，就只能这样表示 ±1.****** x 2ⁿ ，又由于我们把符号位单独用符号数表示了，剩下的尾数部分小数点前面一定是 1”，一定有这个 1 在，无论小数点怎么挪，也表示不了 0.0 这个实数，目前能表示的最小实数用二进制科学记数法表示为： -1.0 x 2^-126，这个数虽然很小很小了，但是依然不为 0。既然用 ±1.****** x 2ⁿ 永远也表示不了 0，那就定义一个例外吧。

这个例外就是：当*阶码为 0 *时，有效数的前面隐含的不再是 1. 而是隐含 0.。

这时候如果有效数也为 0，那么就表示实数 0.0，具体是 -0.0 还是正 +0.0，取决于符号位。

练习

浮点数的基本内容到此结束。现在做一些练习巩固下知识

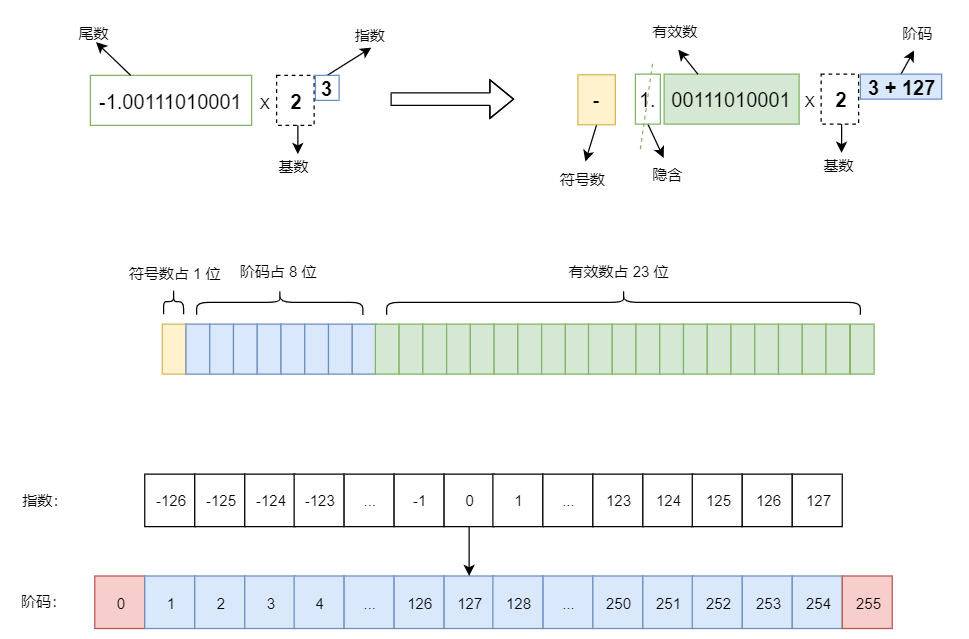
• 练习 1：单精度浮点数 -314.125 是如何储存的

  第一步，先转换成二进制： -100111010.001

  第二步，用科学记数法表示： -1.00111010001 * 2⁸

  第三步，进行规格化：符号数是 1；阶码 = 8+127 = 135，135 的二进制是 10000111；有效数 = 00111010001；

  第四步，达不到储存位宽的填充 0 ：1 10000111 00111010001000000000000

• 练习 2：单精度浮点数 -0.0 是如何储存的

  不用表示成科学记数法就能直接看出：符号数 1；阶码：0000 0000；有效数 0000 0000 0000 0000 0000 000

  所以答案是：1 00000000 00000000000000000000000

但是你以为这就完了吗？No，No，No。

非规格化表示

上面介绍的浮点数表示方法差不多够日常使用了，但是还不够完美。

首先先说下什么是规格化，如上面单精度浮点数，将一个二进制浮点数用科学记数法表示，然后将正负号用符号数表示，尾数省略掉前面的 1. 就变成了有效数，指数加上 127 就变成阶码，这个过程就叫做规格化。

什么又是非规格化呢？当阶码为 0 时，有效数的前面隐含的不再是 1. 而是隐含 0. 且这时指数固定为 -126。这样的表示就是非规格化。前面实数 0.0 就是用非规格化表示的，但表示 0.0 只是非规格化的一部分，还有一部分没介绍。

要介绍这部分涉及到两个术语，突然式下溢、渐进式下溢，但我发现单纯用语言描述这两个东西非常抽象。

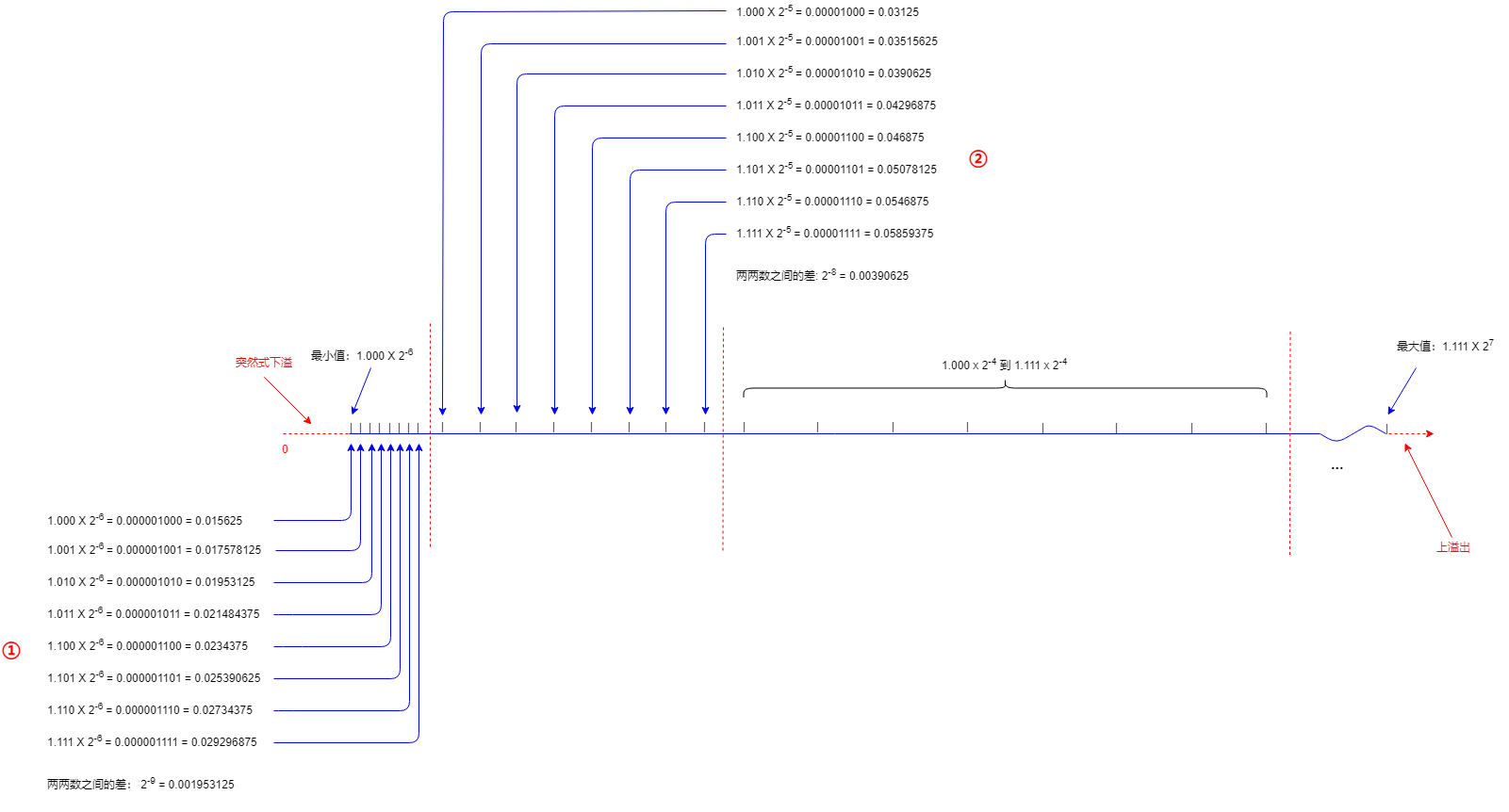
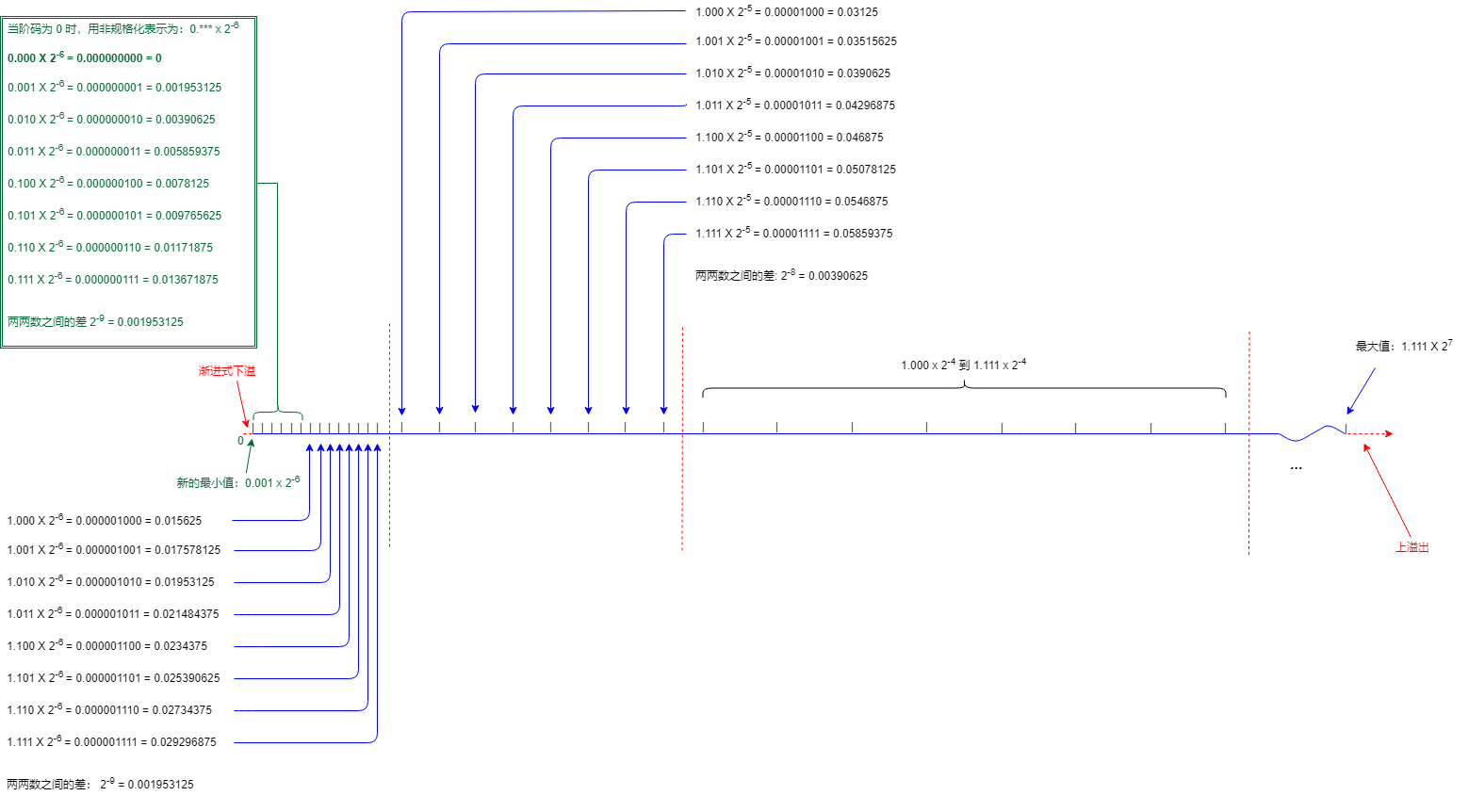
所以我决定根据上面的浮点数表示方式，依样画葫芦，我们只用 8 比特来存储浮点数，因为这样能表示的范围小得多，我们可以把每个数都罗列出来，这样便可以清楚的看到每个具体的数。

以下是我们自己定义的浮点数的储存格式：

符号数依然用 1 位表示。

阶码只使用 4 位，那表示的范围就是 0~15 这 16 个数，中间数是 7 和 8 依然是选其中一个表示 0 都可以，然后正负数向两边延申，这里也是选择 7。

有效位只使用 3 位表示，方便我们罗列出所有的数。

下面这张图画出了指数为 -6 和 -5 时，二进制科学记数法各个数在数轴上的位置，我们只需要关心这部分即可。

也就是 1.000 x 2^-6 到 1.111 x 2^-6 这八个数，如序号 ① 处，和 1.000 x 2^-5 到 1.111 x 2^-5 这八个数如序号 ② 处。

从图中我们可以看出什么？

• 因为有效位只用 3 位表示，所以指数一定时，能表示 8 个数，也就每八个数为一组。
• 每组间八个数两两间的距离是相同的。
• 精度越高的那组八个数中，数于数之间的距离越近。和尺子相似，毫米刻度间的距离比厘米间的距离近，所以毫米的精度更高。

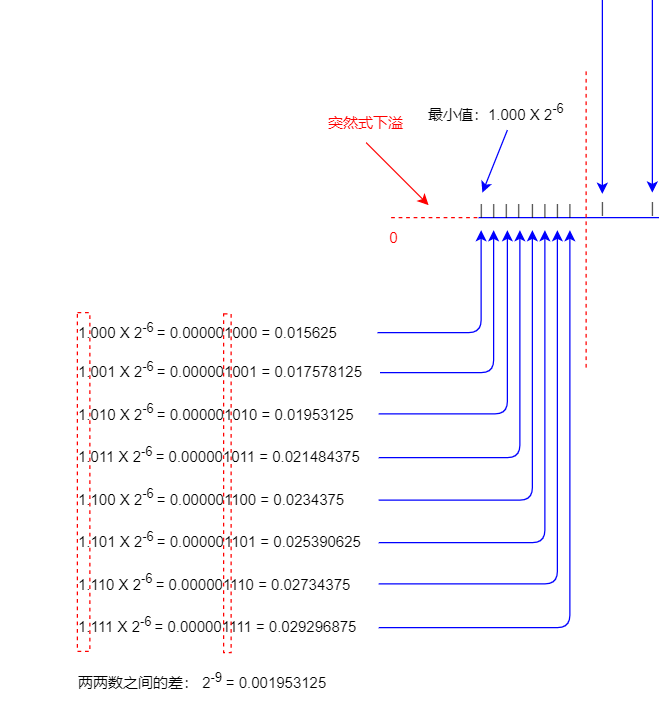
现在说下突然式下溢是什么意思：下溢和上溢都是溢出，即数的大小超出了能储存的范围，比如现在最小值用二进制科学记数法表示是 1.000 x 2^-6，当小过这个数时就不能再储存了。

那为什么前面要加个突然呢？

在 IEEE 754 中，如果下溢出，那么结果将返回 0。指数相同时每组内各个数间距离相同，我们假设序号 ① 那里每个数的间距是 1cm，把它当作一把尺子看。那么这把尺子的刻度就会是这样：0.9、0.8、0.7、0.6、0.5 然后突然到 0，中间的 0.4、0.3、0.2、0.1都没有。

那是什么原因 0.4、0.3、02、0.1 没了呢？

就是因为二进制科学记数法中是固定 1. 开头的，指数是 -6 时，最小数的二进制不是 0.00000 0001 而是 0.00000 1000。

也就是本来应该是从 0.0 到 0.00000 0001 的，现在突然跳到 0.00000 1000。

有什么办法把这些数补回来呢？

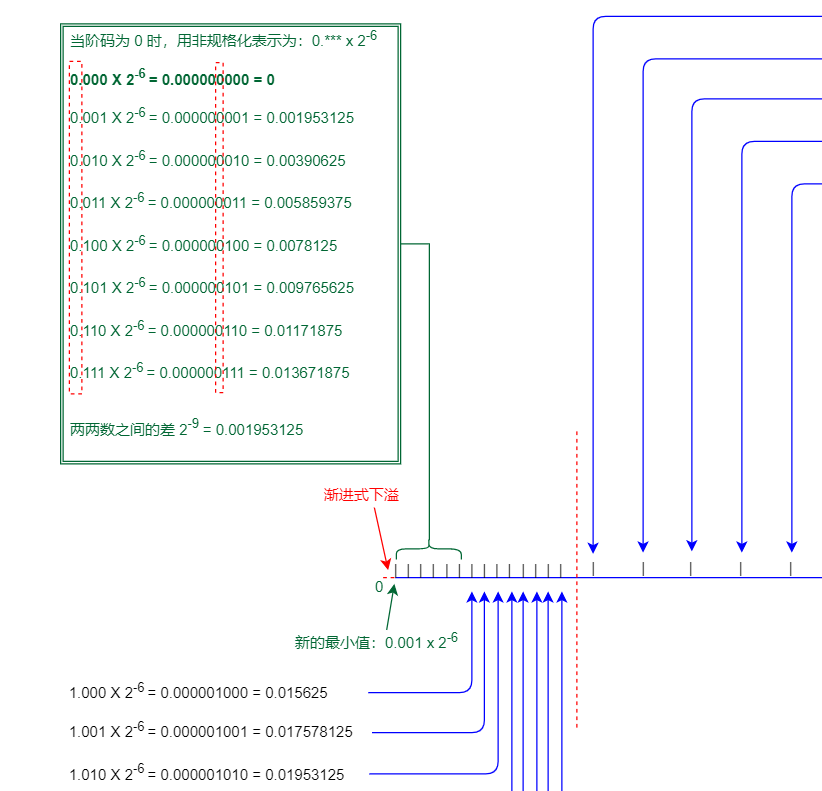
前面知道，阶码为 0 时用作特殊用途，这时有效数前面隐含的是 0. 而不再是 1.

阶码为 0 且有效数为 0 的时候，那它表示实数 0.0。

阶码为 0 有效数不为 0 的时候，我们可以用它来继续表示其他实数。

这时可以用非标准的二进制科学法表示一个实数成这样：0.*** x 2^-6

注意，这里的指数依然是 -6 而不是 -7，如果是 -7 的话，就不能和前面的指数为 -6 这组数，等距的在一个区间，即不能平滑的过度到 0。

所以你就明白为什么 IEEE 754 定义*单精度浮点数非规格化时指数是固定的 -126 *而不是 -127 了。

现在依然会下溢出，只不过引入非规格化后，能平滑的过度到 0 ，而且能多表示几个更小的数（精度没有提高依然是 -6）。

继续拿尺子那里做例子，由 0.9、0.8、0.7、0.6、0.5 然后突然溢出变成 0，到现在的 0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1，如果还有不能表示的数如 0.09 才会溢出变 0。

从这里我们也可以看出 IEEE 754 中单精度浮点数的阶码的偏移量可以是 127 或 128 都无所谓，因为选 128 的话，那指数最小值是 -127，非规格化时固定指数由 -126 改为 -127 即可。

最后附上一张完整的图：

舍入操作

IEEE 754 定义了四个二进制舍入规则，默认使用第一个，以下假设要舍入到整数部分，用十进制举例：

• 舍入到最接近的值，在一样接近的情况下偶数优先：如 1.5 => 2，2.5 => 2
• 向0舍入（截断）：类似强制类型转换。(int) 3.14 = 1，(int) -3.14 = -1;
• 向负无穷大（向下）舍入：类似floor()函数，例如：floor(3.14) = 3，floor(-3.14) = -4。
• 向正无穷大（向上）舍入：类似ceil()函数，例如：ceil(3.14) = 4。Ceil(-3.14) = -3;

偶数优先的原因：

主要是考虑到一组数的时候，比如 1.5、2.5、3.5、4.5，如果都是四舍五入的话变成 2、3 、4、5 会使得这组数的平均值整体拉高。如果一样接近时向偶数舍入，则变成 2 2 4 4，则会有一半的数被拉高，一般被拉低，这组数的平均值就比较接近原来的。

但这只是偶数优先或奇数优先的原因，这两个最终选偶数优先的原因不详，可能有大佬经过科学验证后觉得偶数更优于奇数。

浮点数的加法

0.1 + 0.2 = ？

先确定 0.1 和 0.2 的真实值

0.1 的二进制 0.0001 1001 1001 1001 1001 1001 1001 ….

用二进制科学表示法表示 1.1001 1001 1001 1001 1001 1001 …. x 2^-4

有效数只能存 23 位，这时最接近 0.1 的两个数：

​ 1.1001 1001 1001 1001 1001 100 x 2^-4 = 0.0999999940395355224609375

​ 1.1001 1001 1001 1001 1001 101 x 2^-4 = 0.100000001490116119384765625

取绝对值比较这两个数那个更接近 0.1

​ |0.0999999940395355224609375 - 0.1| = 0.0000000059604644775390625‬

​ |0.100000001490116119384765625 - 0.1| = 0.000000001490116119384765625‬

​ 0.0000000059604644775390625 > 0.000000001490116119384765625

所以 0.1 的近似值取 1.1 1001 1001 1001 1001 1001 101 x 2^-4

用 IEE754 表示：符号数 0；阶码 = -4 + 127 = 123，其二进制 0111 1011；有效数：10011001100110011001101；

0.2 的二进制 0.001 1001 1001 1001 1001 1001 1001 ….

用二进制科学表示法表示 1.1001 1001 1001 1001 1001 1001 …. x 2^-3

有效数只能存 23 位，这时最接近 0.2 的两个值：

​ 1.1001 1001 1001 1001 1001 100 x 2^-3 = 0.199999988079071044921875

​ 1.1001 1001 1001 1001 1001 101 x 2^-3 = 0.20000000298023223876953125

取绝对值比较这两个数那个更接近 0.2

​ |0.199999988079071044921875 - 0.2| = 0.000000011920928955078125

​ |0.20000000298023223876953125 - 0.2| = ‬0.00000000298023223876953125

​ 0.000000011920928955078125 > ‬0.00000000298023223876953125

所以 0.2 的近似值取 1.1001 1001 1001 1001 1001 101 x 2^-3

用 IEE754 表示：符号数 0；阶码 = -3 + 127 = 124，其二进制 0111 1100；有效数：10011001100110011001101；

运算过程模拟

• 读取有效数并将前面的隐含的 1 位补回来得到尾数，读取阶码并减去 127 后得到指数。

  用二进制科学表示法表示为：

  0.1：1.1 1001 1001 1001 1001 1001 101 x 2^-4

  0.2：1.1001 1001 1001 1001 1001 101 x 2^-3

• 对阶（对齐指数）

  小阶对大阶可以使得舍入操作时精度损失更少，对阶相当于移动小数点，把它们的小数点对齐，有效数就能执行加法了

  所以 0.1 的指数 -4 要和 0.2 的指数 -3 一致：

  1.1001 1001 1001 1001 1001 101 x 2^-4 => 0.1100 1100 1100 1100 1100 1101 x 2^-3

• 舍入

  有效数部分只能存储 23 位，加上前面隐含的 1 位，共 24 位，对阶后第 25 位的 1 将执行舍入操作

  此时 0.1100 1100 1100 1100 1100 1101 x 2^-3 = 0.100000001490116119384765625

  两个最接近原来值的数：

  ​ 0.1100 1100 1100 1100 1100 110 x 2^-3 = 0.0999999940395355224609375

  ​ 0.1100 1100 1100 1100 1100 111 x 2^-3 = 0.10000000894069671630859375

  取绝对值比较这两个数那个更接近 0.100000001490116119384765625

  ​ |0.0999999940395355224609375 - 0.100000001490116119384765625| = 0.000000007450580596923828125

  ​ |0.10000000894069671630859375 - 0.100000001490116119384765625| = 0.000000007450580596923828125‬

  发现，这两个数一样接近，根据舍去规则，偶数有先（最低位为 0 的是偶数）。

  所以取 0.1100 1100 1100 1100 1100 110 x 2^-3

• 有效数执行加法

  

  即：10.0110 0110 0110 0110 0110 011 x 2^-3

• 用二进制科学记数法表示

  10.01100110011001100110011 x 2^-3 => 1.0011 0011 0011 0011 0011 0011 x 2^-2

• 舍入

  又多出了一位，要进行舍入操作

  此时 1.0011 0011 0011 0011 0011 0011 x 2^-2 = 0.29999999701976776123046875

  两个最接近原来值的数：

  ​ 1.0011 0011 0011 0011 0011 001 x 2^-2 = 0.2999999821186065673828125

  ​ 1.0011 0011 0011 0011 0011 010 x 2^-2 = 0.300000011920928955078125

  取绝对值比较这两个数那个更接近 0.29999999701976776123046875

  ​ |0.2999999821186065673828125 - 0.29999999701976776123046875| = 0.00000001490116119384765625

  ​ |0.300000011920928955078125 - 0.29999999701976776123046875| = 0.00000001490116119384765625

  发现，这两个数一样接近，根据舍去规则，偶数有先（最低位为 0 的）。

  所以取 1.0011 0011 0011 0011 0011 010 x 2^-2 = 0.300000011920928955078125

• 验证

  所以 0.1 + 0.2 = 0.300000011920928955078125

  但是我用 java 来实验了下（所用代码放在最后面），输出的答案是：

  Code

  最接近 0.1f 的值：        0.100000001490116119384765625
  最接近 0.2f 的值：        0.20000000298023223876953125
  两者相加的精确值：         0.300000004470348358154296875（这个值二进制也无法精确表示）
  
  JAVA 的 0.1f：           0.100000001490116120000000000
  JAVA 的 0.2f：           0.200000002980232240000000000
  JAVA 的 0.1f + 0.2f：    0.300000011920928960000000000

  结果和我们手算的差不多。不知道为何，IEEE 754 单精度浮点数明明有能力精确到 0.300000011920928955078125 类似这样的长度，但是 java 会把它输出为0.300000011920928960000000000 这样的长度。

浮点数运算产生误差的原因

• 有些小数本身就无法用有限位表示

  比如上面加法运算的例子的 0.1 和 0.2 本身就是不精确的。

  这和十进制无法用有限位来表示 1/3、1/7等无限循环小数一样，二进制也无法用有限位来表示1/5、1/10等分数。

• 运算中或运算后会丢失精度

  比如上面加法例子中对阶时丢失精度，运算结束时规格化又再次丢失精度。

举例：

• 8388607.5 + 1 = ？

  8388607.5 和 1 都是能精确表示的，但是结果却是 8388608.0

  8388607.5 用二进制科学表示法表示：1.111 1111 1111 1111 1111 1111 x 2²²

  8388608.5 用二进制科学表示法表示：1.111 1111 1111 1111 1111 1111 1 x 2²³

  当数值到达 8388608 时，整数部分就已经把 23 位有效数全占了，末尾的 1 无法储存

  即指数大于 23 之后，小数部分被丢弃，只能用来表示整数。

• 16777216 + 1 = ？

  16777216 和 1 都能精确表示，但是结果却是 16777218

  16777216 二进制科学表示法表示：1.0000 0000 0000 0000 0000 000 x 2²⁴

  指数 24，相当于有效数后面还要补 0，这时有效数加 1，整体数值不再是加 1 了：

  1.0000 0000 0000 0000 0000 000 x 2²⁴ =>二进制：10000 0000 0000 0000 0000 000 0.0

  这时候有效数部分加 1：10000 0000 0000 0000 0000 001 *0.0 *，表示的数已经加 2 了。

  即指数大于 23 之后，有效数每加 1，整数值就加 2^指数-23 ，不再是加 1 了，导致有的整数也表示不了。

习题

java

public static void main(String[] args){
   	float f1 = 1000000000.0f + 0.5f;
    float f2 = 10f + 1000000000.0f - 1000000000.0f;
    float f3 = 10f + (1000000000.0f - 1000000000.0f);
    
    System.out.println(f1);
    System.out.println(f2);
    System.out.println(f3);
}

以上 java 代码输出什么？答案是：1000000000.0、0 、 10。

原因是：

1000000000.0 用二进制科学表示法表示：1.11011100110101100101000 x 2²⁹，指数是 29 即整数部分已经把有效数的 23 位存储空间全占了，已经无法表示小数部分了，加上任何小数相当于没加，所以 f1 依然输出 1000000000.0。

1000000000.0 下一个能表示的数用二进制科学表示法表示：1.11011100110101100101001 x 2²⁹，这个数是十进制的 1000000064.0，1000000000.0 上一个能表示的数用二进制科学表示法表示：1.11011100110101100100111 x 2²⁹，这个数是十进制的 999999936.0，现在10f + 1000000000.0f 本来应该等于 1000000010.0，但是表示不了，只能取最接近 1000000010.0 的，最接近的依然是 1000000000.0，所以 f2 输出 0。

f3 输出 10 就简单了，加了括号后先算括号内的，再算括号外的。

从这里也看成浮点数运算很多运算法则都无法保障，使用时需要注意。

看完本文后要能回答以下问题

• 阶码为什么使用移码，而不是原码、反码、补码

  为了能直接使用指数比较实数的大小，原码、反码、补码因为符号位原因不好比。

  但是实数本身也带有符号位，既然都要处理一次符号位了，那多处理一次不行吗：可能是比较两次符号位更复杂吧。

  非规格化时，单精度浮点数的指数已经固定 -126 了，又如何比较两个非规格化的实数大小：和规格化一样，先比较符号位，符号位相同再比较阶码，阶码相同再比较有效数，有效数直接从最高位开始比即可。

  一个非规格化的实数如何和一个规格化的实数比大小：符号位相同时，这个肯定规格化的实数大。

• 阶码偏置值为什么是 127 而不是 128

  选 127 或 128 都是可以的，选 127 那表示的范围更大，选 128 精度更高，但是又引入了非规格化使得能表示更小的数了，将这一位用来表示更大范围是合理的。

• 什么是规格化

  具体看上面非规格化部分描述

• 什么是非规格化

  具体看上面非规格化部分描述

• 非规格化的固定指数是 -126 而不是 -127 的原因

  具体看上面非规格化部分描述

• 非规格化的三个好处

  能表示 0.0

  能表示比规格化更小的数，也就是 0.0 到 1.0 x 2^-126 中间还能表示更小的数

  解决突然式下溢，使得 0 到规格化表示的最小数之间更平滑。

• 突然式下溢和渐进式下溢的区别

  具体看上面非规格化部分描述

• 为什么需要无穷大（INFINITY）、NaN（非数）

  NaN：比如求 -4 的平方根，很明显 -4 没有平方根所以它的平方根不是一个数，或 0/0 也是非数

  INFINITY：无穷大，就是超出了浮点数的表示范围叫上溢出，比如 1/0

• Quiet NaN 与 Signaling NaN 两种非数的区别

  安静的非数（Quiet NaN）：安静的NaN就是不会引起错误并且将其自身转换为字符串而继续执行代码

  信令的非数（Signaling NaN）：将引发或设置错误以供用户处理，大多数强类型语言都使用信令NaN

  当一个操作导致一个 Quiet NaN，中途不会得到任何异常指示，直到程序检查结果并看到一个NaN。也就是说，浮点运算将继续进行，不会得到来自浮点单元（FPU）的任何提示信号。

  Signaling NaN 将产生一个信号，通常以浮点单元FPU异常的形式产生该信号。

• 为什么整型没有无穷大和非数

  因为整数是用补码表示，相当于有模运算，即使溢出也“照样能存”，具体看补码那篇文章

• 为什么整型除以0会抛异常但是浮点型不会抛

  原因就是非数是 Quiet NaN

• 为什么用有的浮点数做运算会得到错误结果，如 0.1 + 0.2 != 0.3

  看浮点运算产生误差的原因那部分

• 什么是精度

  指数越小，两个相邻数之间的间距也越小，具体看那张图。

• 为什么 Float.MAX_VALUE + 1 == Float.MAX_VALUE 返回 true

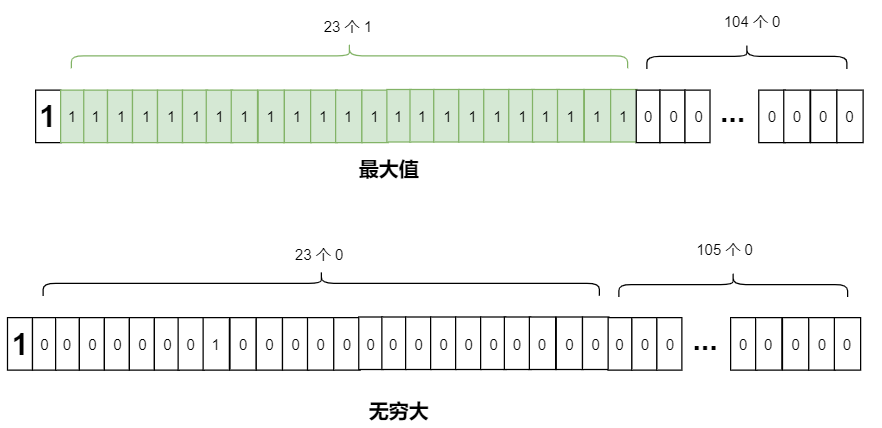
  Float.MAX_VALUE 用二进制科学表示法表示：1.11111111111111111111111 x 2¹²⁷

  它上一个能精确表示的数用二进制科学表示法表示：1.11111111111111111111110 x 2¹²⁷

  它下一个能表示精确表示的数用二进制科学表示法表示：1.00000000000000000000000 x 2¹²⁸ （Infinity）

  加 1 操作对于 127 这么大的量级指数来说，这个数完全达不到它下一个能表示的值，所以只能进行舍入操作

  取一个最接近 Float.MAX_VALUE + 1 的值，这个值依然是 Float.MAX_VALUE

• 为什么 Float.MAX_VALUE + 1 不是 Infinity

  最大值用二进制科学表示法表示：1.11111111111111111111111 x 2¹²⁷

  无穷大用二进制科学表示法表示：1.00000000000000000000000 x 2¹²⁸

  用二进制表示：

  

  要想达到无穷大级别，最大值后面要把 104 个 0 全填充为 1 然后再加 1，也就是要加上 2¹⁰⁴ 才会到达无穷大。但由于有舍入规则，只达到 2¹⁰⁴ / 2 = 2¹⁰³ ，即可达到无穷大。但 2¹⁰³ 的表示也有舍入规则，也就是只要加上一个舍入后为 2¹⁰³ 的值即可达到无穷大。

  比如 10141204500000000000000000000000f 这个数是小于 2¹⁰³（10141204801825835211973625643008）的，但是它被舍入为 2¹⁰³，加上这个数也能达到无穷大。

• 单精度浮点数和双精度浮点数的取值范围（这里讨论不包括 0、非数、无穷大，且只讨论正数）

  单精度最小值用二进制科学表示法(非标准)表示：0.0000 0000 0000 0000 0000 001 x 2^-126

  单精度最小值用二进制科学表示法表示：1.11111111111111111111111 x 2¹²⁷

  双精度类型。

TODO

• BCD 码、BigDecimal的原理

• 浮点数和 BigDecimal 的优势和弱势在那里？

  比如浮点数的运算速度应该比 BigDecimal 的速度快得多，毕竟直接对二进制操作不用缩放。

定点数补充

上述的定点数采用了类似原码的表示方式，实际中定点数可能并不会这么表示，这里只是举例。

实际中的定点数一般也只用来表示纯定点整数或纯定点小数，而且一般采用补码来储存。也就是我们普通的整数和纯小数，既有整数部分又有小数部分的实数一般用浮点数表示，浮点数的运算有自己的浮点运算单元而不和整数共用。

从图中可以看到，纯定点小数和纯定点整数的存储是一模一样的。

纯定点小数用补码表示时的取值范围

纯定点整数就是我们常见的普通有符号整数，现在储存位宽是 16 位，他用补码来表示的范围从 -32768 到 32767，这个很好理解。

那纯定点小数在储存位宽是 16 位时的补码能表示范围是多少呢？

纯定点整数的最小值的补码是 1000 0000 0000 0000 表示十进制 -32768，现在将他缩小 2¹⁵ 倍，-32768 / 32768 = -1

纯定点整数的最大值的补码是 0111 1111 1111 1111 表示十进制 32767，现在将他缩小 2¹⁵ 倍，32767 / 32768 = 0.999969482421875，也就是 1- 1/2¹⁵ = 1 - 0.000030517578125 = 0.999969482421875

这里为什么是缩小 2¹⁵ 倍而不是 2¹⁶ 倍呢：因为这里相对于补码来讨论，而不是纯二进制来讨论。

知道一个纯定点小数，如何快速求它的补码呢？如 -0.125

先放大到 2^存储位宽 倍： -0.125 * 2¹⁶ = -8192

-8192 的补数：2¹⁶- 8192 = 57344

所以 -8192 的补码就是 57344 的二进制 1110 0000 0000 0000‬，也就是 -0.125 的补码

反过来知道纯定点小数的补码 1110 0000 0000 0000 求它表示十进制数：

直接将 1110 0000 0000 0000 转换成十进制的 57344

最高位是 1， 所以这个补码应该表示的是负数，负数的绝对值 = 模数 - 补数 = 2¹⁶ - 57344 = 8192，所以这个负数是 -8192

然后将 -8192 缩小 2¹⁶ 倍：-8192 / 2¹⁶ = -0.125

纯定点小数如何做加法

比如 0.5+0.25+0.125，它们的二进制是 0.1、0.01、0.001，但是真实存到内存时是经过放大了的，比如我们可以先把它们放大 8 倍，也就是左移 3 位，变成二进制的 100+010+001，加起来得二进制 111。然后缩小 8 倍，也就是右移动 3 位，得到 0.111，也就是 0.875 。所以定点小数和整数一样的存法，只不过显示给我们人看时，在缩放指定倍数即可。比如纯定点小数 0.5 和整数 4 的存放一模一样。

但是这只是理想结果，有的小数二进制是表示不了的，缩放倍数选不好会导致误差变更大：

0.1 的二进制约为：0.0001100110011001100110011001100110011001100110011001101

0.2 的二进制约为：0.001100110011001100110011001100110011001100110011001101

0.3 的二进制约为：0.0100110011001100110011001100110011001100110011001101

然后我们只缩放 2⁸ 倍，也就是左移动 8 位：

00011001+00110011+01001100 = 1001 1000 即 25+51+76 = 152，然后 152/256 = 0.59375，虽然原来结果也不得 6，但是肯定和原来的结果也有误差，因为省略了那么多位，也能发现缩放得越大可能误差就越小。

疑惑：定点数历史上真没有用来表示过实数吗？如果有，那如何做加减法？

脚注

[^1]:为什么是 0.9921875 呢？0.5、0.25、0.125、0.0625、0.03125、0.015625、0.0078125的和就是这个值，也就是 二分位、四分位、八分位、十六分位、三十二分位、六十四分位、一百二十八分位这七个分位全为1时表示的小数部分的和，也就是 1/2¹ + 1/2² + 1/2³ + 1/2⁴ + 1/2⁵ + 1/2⁶ + 1/2⁷ = 1 - 1/2⁷ = 0.9921875。
[^2]: 这里的转换只是将整数部分和小数部分单纯的转换成二进制，然后前面添加一个负号，没有经过任何原码，反码，补码等编码。整数部分 314 的二进制为 100111010 你可能会理解，小数部分 0.125 的二进制为什么是 001 呢？我们分别写出十进制的展开式和二进制的展开式子你就明白了。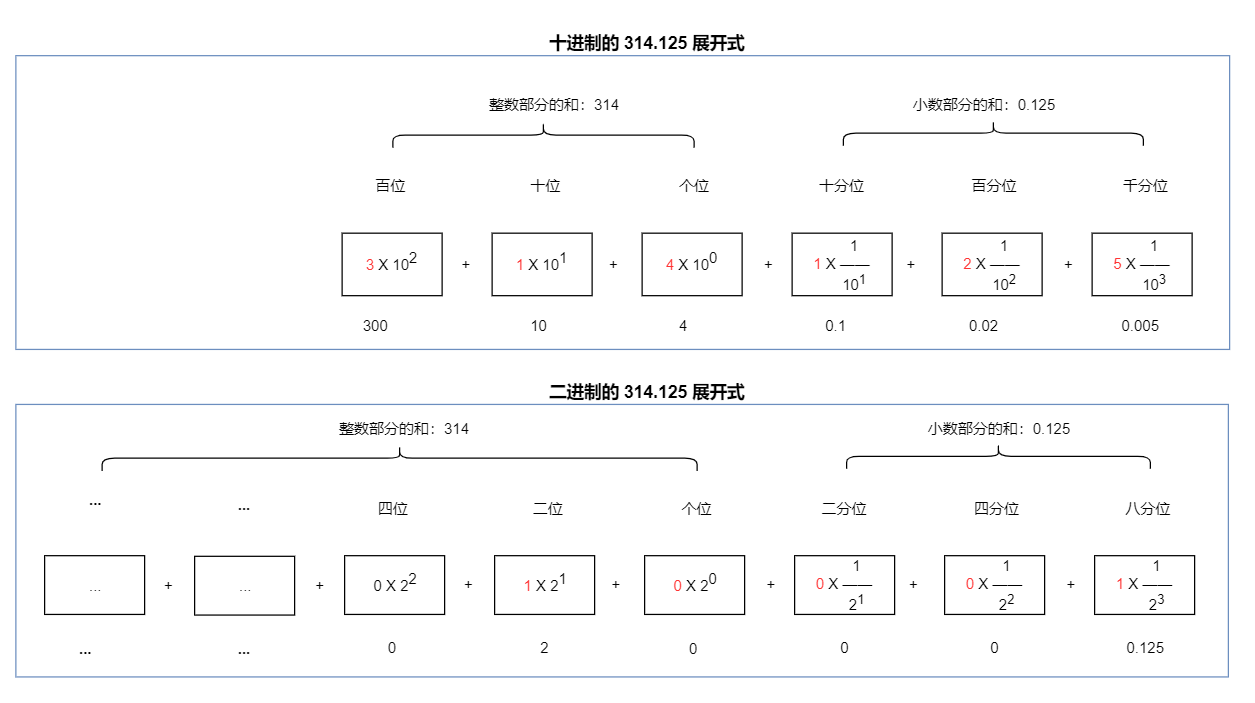

[^3]: 因为最大精度就是一百二十八分位，表示的值是 0.0078125 ，也就是只能保留七位小数（为什么？你想象一下现在小数位最长的数是0.0078125，它加上其他分位，也就是其他小数位比它更短的数，能得到更长的小数位吗？当然不行），超过部分表示不了，可是整数部分还有很多空位。

附录

一个可以直观看浮点数如何存储的网站：https://float.exposed/

获取一个浮点数精确值代码，比如 0.1f 的精确值是 0.100000001490116119384765625

java

package com.bytetest;

import java.math.BigDecimal;

public class Test {
    public static void main(String[] args){

        BigDecimal bigDecimal1 = _获取浮点数的真实值(0.1f);
        BigDecimal bigDecimal2 = _获取浮点数的真实值(0.2f);
        System.out.println("最接近 0.1f 的值：       "+bigDecimal1);
        System.out.println("最接近 0.2f 的值：       "+bigDecimal2);
        System.out.println("两者相加的精确值：       "+bigDecimal1.add(bigDecimal2));

        System.out.printf("JAVA 的 0.1f：           %.27f\n",0.1f);
        System.out.printf("JAVA 的 0.2f：           %.27f\n",0.2f);
        System.out.printf("JAVA 的 0.1f + 0.2f：    %.27f\n",0.1f+0.2f);

        System.out.println("");

        BigDecimal bigDecimal3 = _获取浮点数的真实值(0.1);
        BigDecimal bigDecimal4 = _获取浮点数的真实值(0.2);
        System.out.println("最接近 0.1 的值：        "+bigDecimal3);
        System.out.println("最接近 0.2 的值：        "+bigDecimal4);
        System.out.println("两者相加的精确值：       "+bigDecimal3.add(bigDecimal4));
        
        System.out.printf("JAVA 的 0.1：            %.64f\n",0.1);
        System.out.printf("JAVA 的 0.2：            %.64f\n",0.2);
        System.out.printf("JAVA 的 0.1 + 0.2：      %.64f\n",0.1+0.2);

        System.out.println("");

        test();

    }

    public static void test() {

        System.out.println("最接近 0.1f 的二进制：       "+IntToBit(Float.floatToRawIntBits(0.1f)));
        System.out.println("最接近 0.2f 的二进制：       "+IntToBit(Float.floatToRawIntBits(0.2f)));


        System.out.println("");

        System.out.println("最接近 0.1 的二进制：       "+LongToBit(Double.doubleToRawLongBits(0.1)));
        System.out.println("最接近 0.2 的二进制：       "+LongToBit(Double.doubleToRawLongBits(0.2)));
    }


    public static BigDecimal _获取浮点数的真实值(float f){
        int floatToRawIntBits = Float.floatToRawIntBits(f);
       return _二进制字符串转十进制(IntToBit(floatToRawIntBits));
    }

    public static BigDecimal _获取浮点数的真实值(double d){
        Long doubleToRawLongBits = Double.doubleToRawLongBits(d);
        return _二进制字符串转十进制(LongToBit(doubleToRawLongBits));
    }

    private static BigDecimal _二进制字符串转十进制(String _二进制字符串){
        boolean _负数 = false;
        if(_二进制字符串.startsWith("-")){
            _负数 = true;
        }
        String[] s = _二进制字符串.replaceAll("[+,-]","").split("\\.");
        byte[] _整数部分 =s[0].getBytes();
        byte[] _小数部分 =s[1].getBytes();

        BigDecimal  _整数十进制 = new BigDecimal("0.0");
        for(int i=0; i<_整数部分.length; i++){
            if(_整数部分[i] == 49){ //为 1
                BigDecimal x0 = new BigDecimal("2.0").pow(_整数部分.length-1-i);
                _整数十进制 = _整数十进制.add(x0);
            }
        }

        BigDecimal _小数数十进制 = new BigDecimal("0.0");
        for(int i=0; i<_小数部分.length; i++){
            if(_小数部分[i] == 49){ //为 1
                BigDecimal x0 = new BigDecimal("1.0");
                BigDecimal x1 = new BigDecimal("2.0").pow(i+1);
                BigDecimal x2 = x0.divide(x1);
                _小数数十进制 = _小数数十进制.add(x2);
            }
        }
        _整数十进制 = _整数十进制.add(_小数数十进制);
        if(_负数){
            _整数十进制 = new BigDecimal("0.0").subtract(_整数十进制);
        }
        return _整数十进制;
    }
    
    //浮点数 IEEE754 代表的那个整数，转为精确浮点数的二进制字符串形式
    //如单精度：符号数 1 位，阶码 8 位，有效数 23 位，这 32 位看成一个整数
    private static String IntToBit(int raw) {
        StringBuilder _尾数 = new StringBuilder();
        for (int i = 0; i <23; i++) {
            _尾数.append(((raw >> i) & 0x1));
        }
        _尾数.reverse();


        int _阶码 = 0;
        for (int i = 23; i <31; i++) {
            if(((raw >> i) & 0x1) == 1)
                _阶码 += Math.pow(2.0,i-23);
        }

        if(_阶码 == 0){
            _尾数.insert(0,"0");
        } else {
            _尾数.insert(0,"1");
        }

        int _指数 = 0;
        if(_阶码==0 && _尾数.indexOf("1")!=-1){
            _指数 = _阶码 - 126;
        }else {
            _指数 = _阶码 - 127;
        }

        if(_指数>=0 && _指数<=22){
            _尾数.insert(_指数+1,".");
        }else if(_指数 == 23){
            _尾数.append(".0");
        } else if(_指数>23){
            for (int i = 0; i < _指数 - 23; i++) {
                _尾数.append("0");
            }
            _尾数.append(".0");
        }else {
            for (int i = 0; i < Math.abs(_指数); i++) {
                _尾数.insert(0,"0");
            }
            _尾数.insert(1,".");
        }

        if(((raw >> 31) & 0x1) == 1){
            _尾数.insert(0,"-");
        }else {
            _尾数.insert(0,"+");
        }

        return _尾数.toString();
    }

    //浮点数 IEEE754 代表的那个整数，转为精确浮点数的二进制字符串形式
    //如单精度：符号数 1 位，阶码 8 位，有效数 23 位，这 32 位看成一个整数
    private static String LongToBit(Long raw) {
        StringBuilder _尾数 = new StringBuilder();
        for (int i = 0; i <52; i++) {
            _尾数.append(((raw >> i) & 0x1));
        }
        _尾数.reverse();


        int _阶码 = 0;
        for (int i = 52; i <63; i++) {
            if(((raw >> i) & 0x1) == 1)
                _阶码 += Math.pow(2.0,i-52);
        }

        if(_阶码 == 0){
            _尾数.insert(0,"0");
        } else {
            _尾数.insert(0,"1");
        }

        int _指数 = 0;
        if(_阶码==0 && _尾数.indexOf("1")!=-1){
            _指数 = _阶码 - 1022;
        }else {
            _指数 = _阶码 - 1023;
        }

        if(_指数>=0 && _指数<=51){
            _尾数.insert(_指数+1,".");
        }else if(_指数 == 52){
            _尾数.append(".0");
        } else if(_指数>52){
            for (int i = 0; i < _指数 - 52; i++) {
                _尾数.append("0");
            }
            _尾数.append(".0");
        }else {
            for (int i = 0; i < Math.abs(_指数); i++) {
                _尾数.insert(0,"0");
            }
            _尾数.insert(1,".");
        }

        if(((raw >> 63) & 0x1) == 1){
            _尾数.insert(0,"-");
        }else {
            _尾数.insert(0,"+");
        }

        return _尾数.toString();
    }

}