计算机底层为什么使用补码

本篇文章不会像大多数博客或书本上那样先讲原码，再讲反码，最后讲补码。这样好像它们的历史发展就是按照这个顺序来的，谁先出现的顺序还说不准。更不会告诉你补码的计算方式等于什么反码加一，我觉得这有点本末倒置。我将从另一角度尝试解释计算机底层为什么使用补码。

目标

二进制对计算机来说是可运算的最小单位，所有操作终将转换成对二进制的运算，而对二进制的运算可以设计逻辑电路来实现，比如加法器逻辑电路可以对二进制进行加法运算。

上篇文章介绍了加法器的原理，那要做减法、乘法、除法运算是不是还需要分别添加对应的逻辑电路呢？

答案是：可以这么做，但是没必要。我们知道逻辑电路设计得越复杂，那么运算效率越低，成本也会越高。我们设计出了加法运算的逻辑电路，它只能做加法，在不对该电路做任何修改的前提下，如果它也能帮我们做减法题，我们就不用再添加减法逻辑电路，运算效率也就更高了。

我们的目标就是要找到一种方法，在计算机只会做加法的前提下，帮我们做减法题。

思路

如何让一个正数加上另一个正数后结果变得更小呢（也就是相当于减去一个数）。你初想，绝对不可能，但有一种方法可以做到，那就是取模，假设模为16，（10+9）% 16 = 3，结果是不是变小了？

取模后你会发现（10-7）% 16 也等于 3 ，你感觉，可能有戏，既然 （10+9）% 16 和（10-7）% 16 都等于 3，那是不是有可能可以用（10+9）替换掉（10-7），那不就能用加法器做减法题了吗？

模运算问题

可是多了个模16运算，加法器可没这个功能。那是不是要添加模运算的逻辑电路到加法器才行呢？

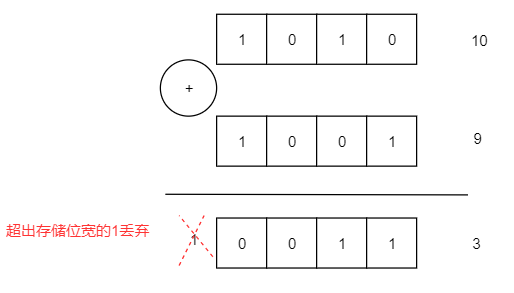
大可不必，你发现，只要我们提前确定好计算结果的存储位宽之后，将超出存储位宽的值丢弃，就相当于有了模运算功能。

比如现在确定用 4 比特来存储计算结果，4 比特只能表示 0~15 这 16个数，当计算结果大于 15 时，相当于取16的模，又重新从 0 开始。

如图，10+9 用 4 比特来存储计算结果时，结果和 （10+9）% 16 一样，都等于 3

疑惑

你现在可能会有四个疑惑

1. 用 4 比特来存储计算结果时，相当于模16，那要是用 8 比特时相当于模多少？
2. 模 16 时 10+9 和 10-7 的结果一样，也就是 -7 可以用 9 来替代表示，为什么是 9，这两个数有什么关系？
3. 如果 -7 用 9 来替代表示了，那 9 怎么表示？
4. 模不是 16 时，比如说是其他的数，还可以用正数表示负数吗？

解惑

第一个问题：用 4 比特来存储计算结果时，相当于模16，那要是用 8 比特时相当于模多少？

这个问题很简单，4 比特能表示 2⁴=16，也就是 0~15 这 16 个数，相当于模 16；

8 比特能表示 2⁸=256，也就是能表示 0~255 这 256 个数，相当于模 256。

第二个问题：模 16 时 10+9 和 10-7 的结果一样，也就是 -7 可以用 9 来替代表示，为什么是 9，这两个数有什么关系？

在模为 16 时，不单有 （10+9）% 16 = （10-7）% 16

还有：

Code

（x-16）% 16  = （x+0）% 16 
（x-15）% 16  = （x+1）% 16 
（x-14）% 16  = （x+2）% 16 
（x-13）% 16  = （x+3）% 16 
 ...
 （x-0）% 16  = （x+16）% 16

x 可以是任意整数，不妨把 x 当 0 看待，即两个整数模同一个数后，余数相同，和数学上同余概念是等价的。

Code

-16 和 0 对模 16 同余

-15 和 1 对模 16 同余

...

所以我们可以在计算机领域这样表示：

模 m 同余的一个正数和一个负数中，可以把正数叫做负数的补数

比如模 16 同余时，-7 的补数是 9

知道一个负数求它的补数也很简单，*负数的补数 = 模数 - 负数的绝对值 *

那正数的补数是不是对应的那个负数呢？在数学上可以说这两个数互为补数，但在计算机领域中我觉得没必要，因为我们的目标是用加法代替减法，同余时用正数代替负数可以实现这一目标，而正数不需要替代，也就是不用补数，或者说正数的补数是它本身。

第三个问题：如果 -7 用 9 来替代表示了，那 9 怎么表示？

在确定储存位宽后能表示的数的范围就确定了，比如确定为 4 比特后能表示的二进制范围就是 00001111，也就是十进制 015。

0~15 这 16 个数，我们完全可以全部用来表示成负数，比如说：

Code

正数  0，看成是 -16
正数  1，看成是 -15
正数  2，看成是 -14
正数  3，看成是 -13
正数  4，看成是 -12
正数  5，看成是 -11
正数  6，看成是 -10
正数  7，看成是 -9
正数  8，看成是 -8
正数  9，看成是 -7
正数 10，看成是 -6
正数 11，看成是 -5
正数 12，看成是 -4
正数 13，看成是 -3
正数 14，看成是 -2
正数 15，看成是 -1

全部表示成负数，照样能得到正确的计算结果，但是你就只能用来计算负数和负数的加法了，比如 -2 + -3，加法器看到的是 （14 + 13）% 16 = 11，11 又被表示成 -5，结果也是对的。

可是全部用来表示成负数之后正数怎么表示？我们得有个取舍吧，我们当然希望能尽可能多的表示正数和尽可能多的表示负数。那就从 0 开始对半分，正数和负数能表示的数都最多。

Code

正数  0，严格来说 0 既不是正数也不是负数，那就还是表示它自己

正数  1，不看成负数，就表示正数 1 
正数  2，不看成负数，就表示正数 2 
正数  3，不看成负数，就表示正数 3 
正数  4，不看成负数，就表示正数 4 
正数  5，不看成负数，就表示正数 5 
正数  6，不看成负数，就表示正数 6 
正数  7，不看成负数，就表示正数 7 

正数  8 ？？？

正数  9，看成是 -7
正数 10，看成是 -6
正数 11，看成是 -5
正数 12，看成是 -4
正数 13，看成是 -3
正数 14，看成是 -2
正数 15，看成是 -1

问题来了，16 个数减去一个用来表示既不是正数也不是负数的 0 后，还有 15 个数，15 是奇数是不能平分的。

分到正数 8 的时候，可以看成是 -8，也可以直接表示 8，那到底表示 -8 好还是 8 好呢？我们用二进制写出 0~15

Code

正数  0 二进制 0000，严格来说 0 既不是正数也不是负数，那就还是表示它自己
        
正数  1 二进制 0001，不看成负数，就表示正数 1 
正数  2 二进制 0010，不看成负数，就表示正数 2 
正数  3 二进制 0011，不看成负数，就表示正数 3 
正数  4 二进制 0100，不看成负数，就表示正数 4 
正数  5 二进制 0101，不看成负数，就表示正数 5 
正数  6 二进制 0110，不看成负数，就表示正数 6 
正数  7 二进制 0111，不看成负数，就表示正数 7 
        
正数  8 二进制 1000，？？？
        
正数  9 二进制 1001，看成是 -7
正数 10 二进制 1010，看成是 -6
正数 11 二进制 1011，看成是 -5
正数 12 二进制 1100，看成是 -4
正数 13 二进制 1101，看成是 -3
正数 14 二进制 1110，看成是 -2
正数 15 二进制 1111，看成是 -1

你会发现最高位是 1 的所有正数都用来表示负数了，8 的二进制最高位也是 1。加法器眼中所有二进制都是正数，但要强行把某些二进制显示成负数给我们人看，为了方便和统一，8 的二进制最高位也是 1，当然选择把二进制 1000 看成 -8 更合理。

同理，现在是 4 比特的存储位宽，4 比特能表示 2⁴=16 个数。当存储位宽是 n 比特时，能表示 2ⁿ 个数，2ⁿ 一定是偶数。然后减去一个用来表示 0 的之后，还能表示 2ⁿ-1 个数，2ⁿ-1 一定是奇数。奇数是不能平分的，就和上面的 8 要表示成正数还是负数一样，最后决定把那个不能平分的二进制表示成负数，所以你就能明白为什么你总看到类似 [-128，127]、[-32768，32767] 等负数能表示的范围比正数多一个的取值范围了。

第四个问题：模不是 16 时，比如说是其他的数，还可以用正数替代负数吗？

从第二个问题解答那里知道，不管模是多少，模确定之后（也就是储存位宽确定后），负数总能用它的补数来替代表示。

总结

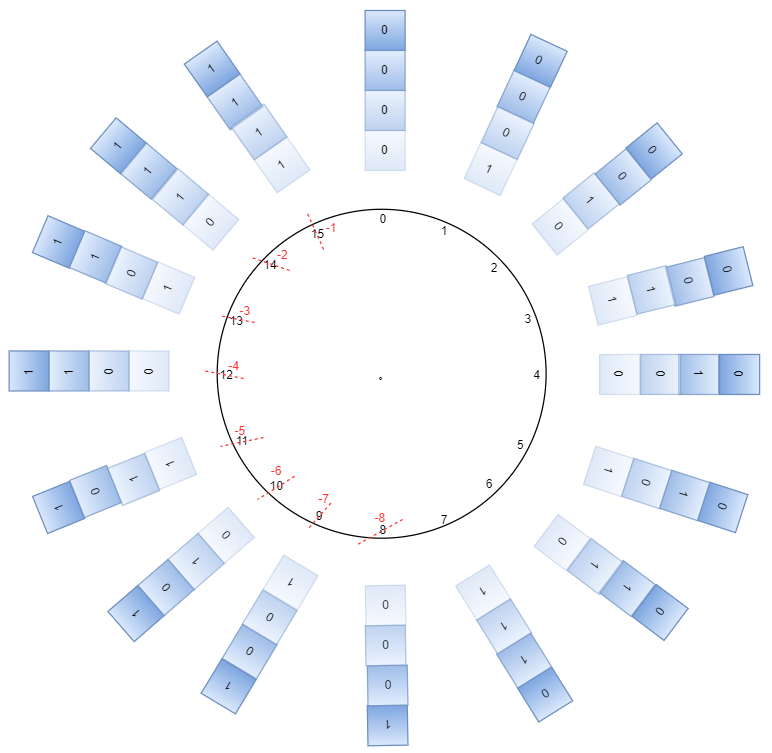
现在我们明白了，加法器固定储存位宽后可以达到模运算的效果，而在模运算中存在同余关系，利用同余关系可以把一个负数用正数替换，也就是可以将减法转换成加法，最终达到使用加法器做减法题的目的。当存储位宽是 4 比特时，加法器看到的二进制表示的数和我们眼中看到的二进制表示的数如下：

加法器眼中，这些二进制只是普通的正数 0~15，如黑色字体表示。我们眼中将部分正数表示成了负数如红色字体所示。

所以什么符号位在加法器眼中统统不存在，你也不用纠结加法器为什么能把符号位参与进运算了，因为在它眼中是根本就没有的概念，符号位是为了方便将普通二进制转换成负数显示给我们人看的。

其他

1. 看完这篇文章后，别人再问如何求一个负数的补码时希望你别再用先求反码后加一来算了，正确的套路应该是：

   先确定存储位宽求得模数，比如 java 中 int 用 32 比特存储，模数就是那么 2³²

   负数的补数 = 模数-负数的绝对值 ，比如 -100 的补数 = 2³² -100 = 4294967196

   也就是 -100 的补码就是 4294967196 的二进制 1111 1111 1111 1111 1111 1111 1001 1100。

   如果你用反码加一来求，当你用逆思维由补码算反码时可能会得到错误的答案，也就是二分时候的那个临界值怎么表示那里。比如存储位宽 4 比特时， -8 的补码 1000，如果逆向思维，补码等于反码加一，那反码就等于补码减一。1000 - 1 = 0111 ，0111 不应该是 7 的反码吗，怎么是 -8 的反码呢？

2. 知道补码如何求它表示十进制数

   比如 1111 1111 1111 1111 1111 1111 1001 1100 ：直接转换成十进制得到 4294967196。

   由于最高位是 1，所以它应该表示负数，这个负数的绝对值 = 模数 - 补数 = 2³²-4294967196 = 100，这个负数就等于 -100

   也就是上面的逆运算而已

3. 为什么补码的英文名是 two‘s complement

   直译就是“二的补”，更好的理解应该是 2ⁿ 的补，n 是存储位宽。也就是模数的补。

4. java 如下代码会输出什么

   java

   public static void main(String[] args){
           byte b;
           for( int i = 0; i <= 255; ++i ){
               b = (byte)i;
               System.out.println(b+", ");
           }
   }

   这段代码的输出会是，先输出 0 到 127，然后输出 -128 到 -1

   原因是 byte 占一个字节，也就是 8 比特，强制转的时候 int 直接把低八位的二进制复制给 byte，打印的时候把这些二进制都当补码看待，所以从打印到 128 的二进制开始就会显示成 -128、-127、-126，直到 -1。

5. 关于网上说的补码解决了“0 有两种表示的问题”和“将减法转换成加法的问题”

   但我觉得“解决 0 的两个表示问题”这一说法是受到了原码和反码这种编码方式中符号位说法的影响，也就是你认为先有原码和反码才有补码，但是可能并不是这样。如果你没有先入为主，提前就有符号位的概念，在探索补码得产生过程中，你就不会把二进制 1000 看成是 -0 呢，又哪来的 0 有两种表示的问题。

TODO

• 原码在计算机中有什么用途？

  目前没有看到原码的应用场景，难道只是一个发展产物吗？

• 反码的发展历史，以及为什么补码 = 反码 + 1？

  虽然有点本末倒置，但依然要了解它们背后的联系和数学原理

• 反码能拿来做运算吗？

  有些博客中说反码不能拿来运算且不能将加法转成减法，这是错误的，反码一样可以用来运算，且能把减法转换成加法，只不过不能丢弃超出存储位宽的位，要把超出的位和得到的结果再次进行加法运算，也就是要多添加一个“循环进位”电路，还有一个缺点就是 0 有两种表示方式，一些老的计算机底层就曾经采用过反码。有时间会写一篇关于下反码的原理。

• 为什么反码的英文名是ones complement

  注意，是 ones complement 而不是 one‘s complement，是全 1 的补，而不是 1 的补，这要结合反码的发展来说。

• 定点数和浮点数如何表示？

• 为什么用浮点数计算结果不准确？

• 乘法和除法是如何通过移位来实现的？

  移位只能是乘或除 2，如果要乘或除的数不是 2 的倍数时怎么做？