按照惯例,本篇文章依然不会像书本那样,给出一堆真值表,然后说什么什么电路可以实现这些真值表,然后就能做出加法器,那是机器的的思考方式不是我们人的。正确的思路应该是人在做加法运算时大脑会做哪些事情,如何使用逻辑电路替代大脑中做的事。
先看一个案例
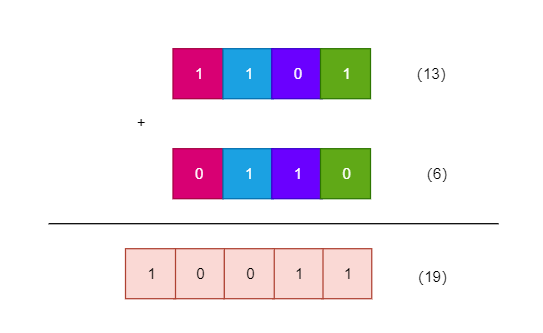
用二进制来计算 13+6
发现很简单,我们大脑中计算这个二进制加法的过程如下:
发现我们的大脑主要做了三件事:
问题一:图中 ? 是一种什么逻辑运算。
光看上图不够清晰明了,下面列举了该种运算的所有可能和结果:
| 位1 | 位2 | 结果 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
答:两者不同得到1相同得到0,这不就是 异或 运算嘛。
问题二:我们是如何判断产生了进位,且这种判断是一种什么逻辑运算。
答:当两者都是1的时候产生进位。很明显,这是一种 与 运算。
半加器
如果要让计算机替我们执行加法运算,那我们就要设计电路实现我们大脑中做加法运算时的那三件事。
从上面的分析知道,要完成前面两件事,只要使用一个异或门和一个与门即可。这种电路又叫半加器。
现在我们尝试使用四个半加器来做 13+6 的加法运算:
然而并不能得到正确的结果,为什么呢?
半加器能做到两个位之间的运算,且能判断两个位在运算后是否会产生进位。而第三件事并没有做到,也就是没有做到如果上一次产生进位,下一次运算要把进位参与进运算来。
它叫半加器的原因:
不能把上一次进位信息输入进半加器,即使使用多个半加器也不能完成两个数的加法运算,只能完成加法运算的一部分,所以叫半加器。
全加器
半加器还差一件事没有做到,那就是把上一次运算产生的进位参与到下一次运算。全加器要实现这一点我们先要思考两个问题
- 上一次的进位会影响到本次异或运算的结果吗?
- 上一次的进位会影响到判断本次运算是否需要进位吗?
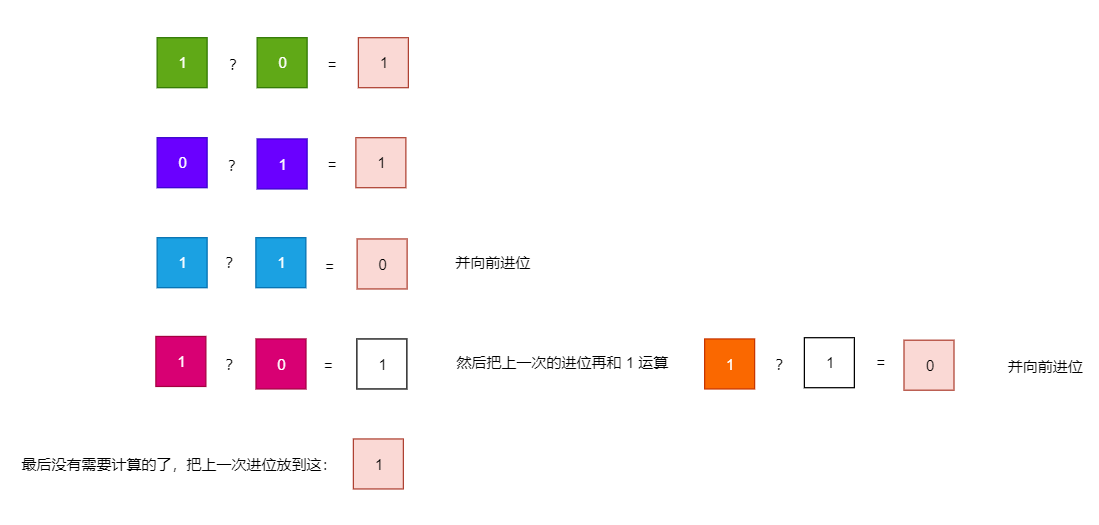
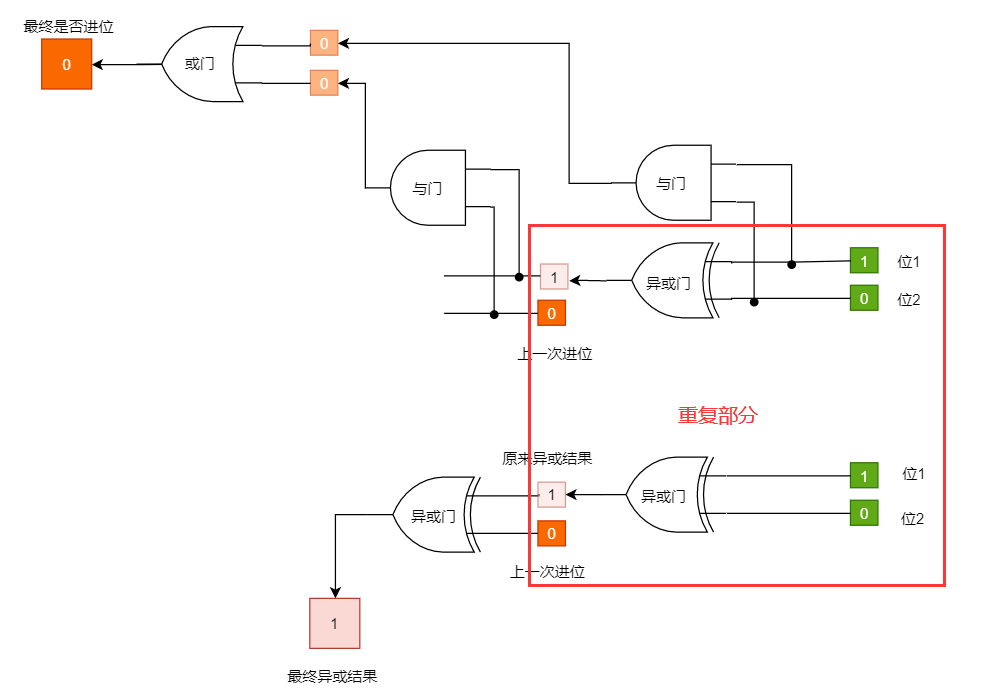
我们继续看上面那一张大脑中是如何计算二进制加法的那张图。
看红框部分,本来只需要运算 1 异或 0 得到 1 ,如序号①
但是由于上一次运算有进位,所以又把得到的结果 1 和上一次进位的 1 进行了一次异或运算得到 0,如序号②
同时我们发现,本来只需要运算序号①部分,是不需要进位的,但由于上一次进位的影响,导致最终需要进位,如绿色框所示。
也就是上面两个问题的答案是:上一次进位信息会影响到本次异或运算的结果且会影响到判断本次运算是否需要进位。
具体是如何影响的?
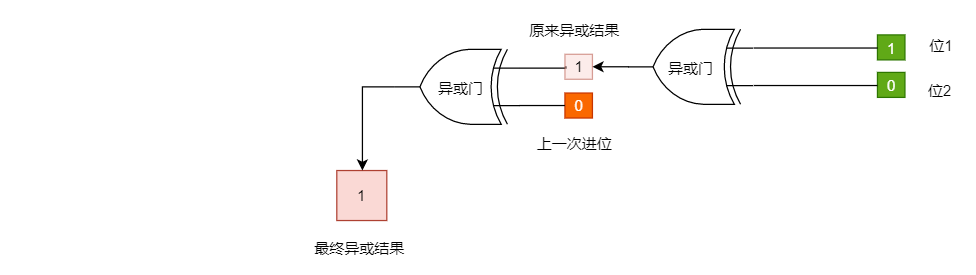
上一次进位对本次异或运算结果的影响
很明显,我们直接把两个位进行异或运算得到结果①,但因为上一次有进位,又把结果①再次和进位的1进行异或运算得到结果②。
也就是上一次运算有进位时会导致我们需要多进行一步异或运算。
那上一次没有进位的时,我们把它的进位值设为0,然后也多进行一步异或运算,还能得到正确的结果吗?
上一次没有进位时,不进行多一次异或运算,正确的运算结果如下:
位1 位2 最终异或结果 0 0 0 0 1 1 1 0 1 1 1 0 上一次没有进位时,把其进位值设为0,然后多进行一步异或运算,结果如下:
位1 位2 第一次异或结果 上一次进位 最终异或结果 0 0 0 0 0 0 1 1 0 1 1 0 1 0 1 1 1 0 0 0 通过对比两表的最终异或结果一栏发现,两者是一致的。
也就是上一次没有进位时其进位值设为0,有进位时其进位值设为1,然后串联两个异或门使上一次的进位参与到本次异或运算中是可行的
上一次进位对判断本次运算是否需要进位的影响
我们很容易就能想到,只有以下两种情况需要进位:
- 两个位都是1时不管上一次是否有进位,本次都会进位
- 两个位其中仅有一个位是1,且上一次有进位时,本次会进位
分析上面的话,将其转换成逻辑电路:
- ”两种情况需要进位“:也就是只要其中一种情况发生就会产生进位,典型的或门电路
- ”两个位都是1时不管上一次是否有进位,本次都会进位“:也就是只关注两个位都为1时,典型的与门电路
- ”两个位其中仅有一个位是1,且上一次有进位时,本次会进位“:前半句“两个位其中仅有一个位是1”典型的异或门电路。后半句“且上一次有进位时”典型的与门电路。也就是两个位先经过一个异或门得到结果1,然后结果1和上一次进位再经过一个与门。
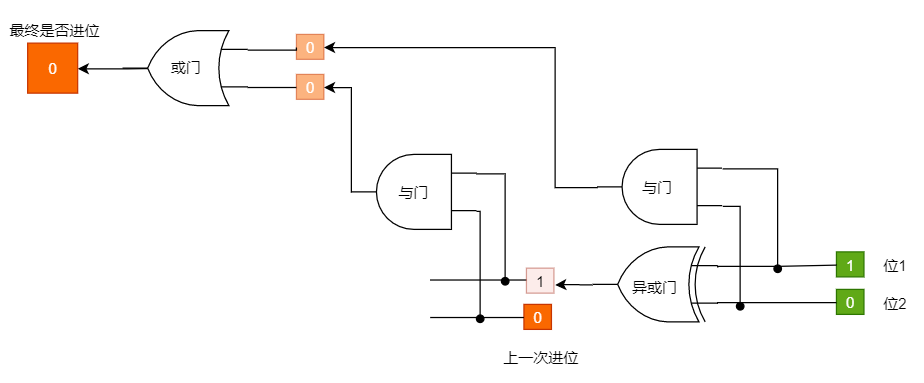
综上判断本次是否需要进位的电路如下:
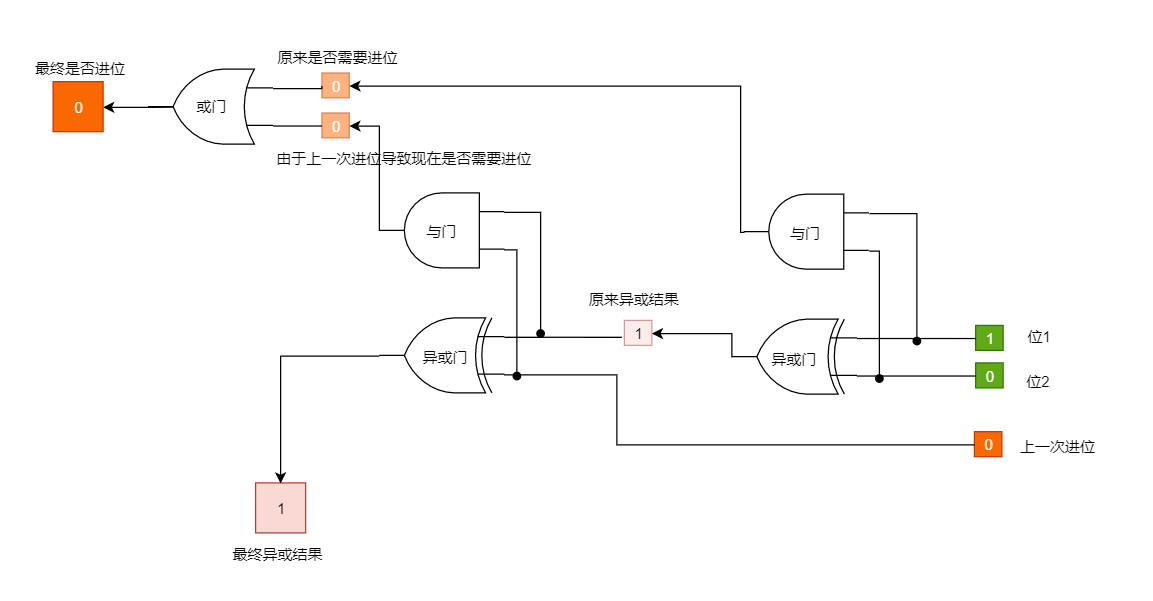
把判断是否需要进位的电路和异或运算电路合并,并去掉重复部分。
我们便得到了一个能把上一次进位信息参与到下一次运算的电路,又叫全加器
一个全加器只能进行一个位的运算,要运算多个位只要把多个全加器连在一起即可。
现在再尝试使用四位全加器来做 13+6 的加法运算(点击可看大图):
得到正确结果:10011 即十进制的 19
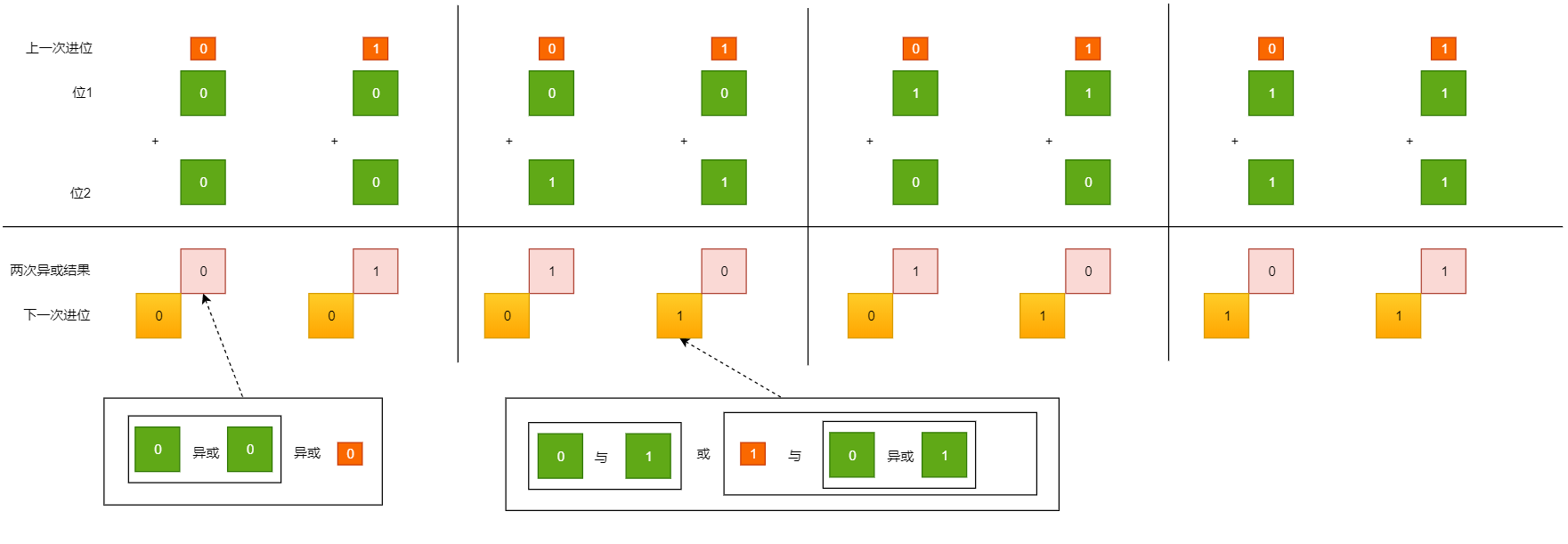
同时附上一张全加器的真值表: