Juchia
Home
Archives
Tags
Categories
Link
About
avatar
文章
27
标签
21
Home
Archives
Tags
Categories
Link
About
目录
  1. 1. 当出现不平衡时我们的想法是什么
  2. 2. 旋转的具体实例
  3. 3. 如何才能知道结点失衡了
  4. 4. 如何判断是哪一种失衡
  5. 5. 代码实现
二叉平衡树的旋转问题

当出现不平衡时我们的想法是什么

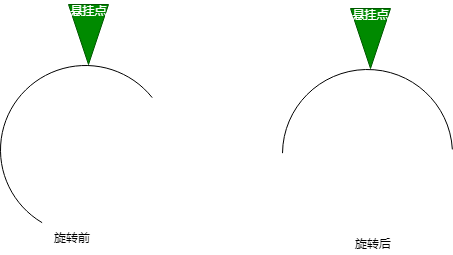
  1. 如图: 左边重, 如何让它保持平衡呢 ?

    平衡二叉树不平衡时的想法.png

    简单, 左边重往右边旋转, 反之右边重往左边旋转

  2. 为了方便说明问题, 将环分用两种颜色标记为两部分

    平衡二叉树不平衡时的想法1.png

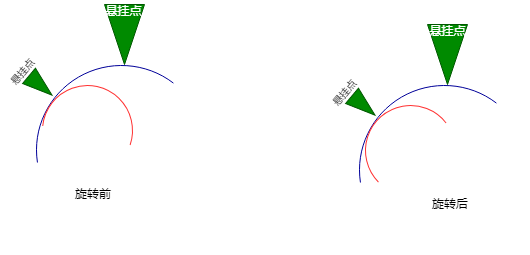
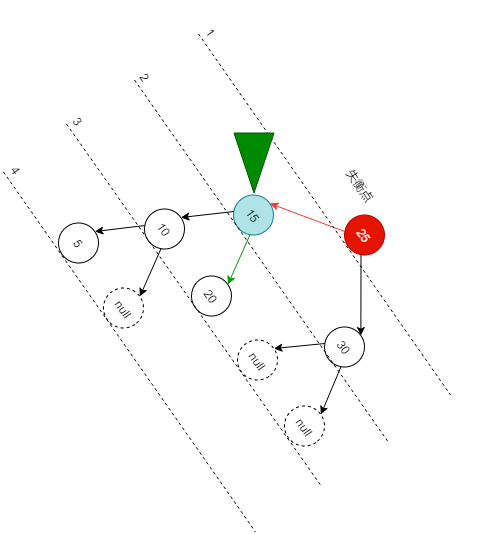
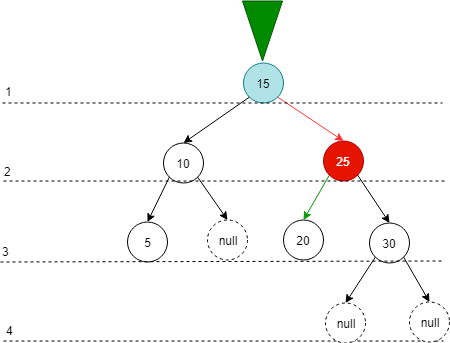
    那下面这种情况该如何平衡呢 ?

    平衡二叉树不平衡时的想法2.png

    按照前面的方法, 左边重往右边旋转. 咦, 怎么旋转后变成右边重了, 如何解决 ?

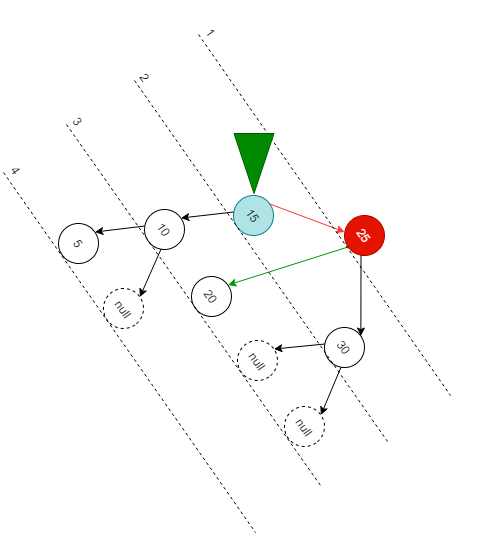
    1. 红线局部部分是右边重, 所以先想办法解决局部部分, 解决办法也很简单, 右边重往左边旋转

      平衡二叉树不平衡时的想法3.png

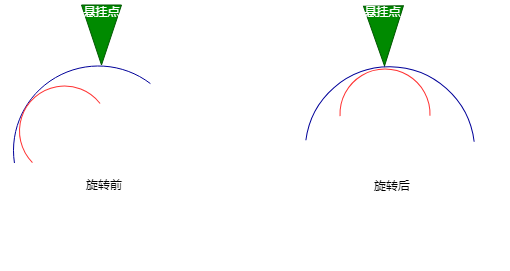
    2. 局部部分解决后, 再解决整体, 解决办法也很简单, 再向右旋转即可

      平衡二叉树不平衡时的想法4.png

  3. 蓝色弧失衡和红色弧失衡可以组合成四种失衡

    • 左左失衡

      只需要整体向右旋转即可

    • 右右失衡

      只需要整体向左旋转即可

    • 左右失衡

      先将局部向左旋转, 然后再将整体向右旋转

    • 右左失衡

      先将局部向右旋转, 然后再将整体向左旋转

旋转的具体实例

思想是有了, 但是上面的图很抽象, 对于真正的二叉树, 还要处理一些细节问题, 以左左失衡为例:

左左失衡1.png

  1. 向右旋转

    左左失衡2.png

    旋转后以下问题需要解决

    • 根结点需要更新
    • 红色的边方向错误, 需要修改
    • 新的根结点有了三个孩子结点(绿色的边), 需要解决

  2. 解决上述三个问题

    • 更新根结点

      这个问题不用处理, 因为使用递归算法, 每次递归结束要返回本次递归的根节点给上层, 只要把新的根结点返回去即可

    • 更新红色的边

      把新的根结点(结点 15)的右孩子设置为失衡结点(结点 25)即可

    • 解决新的根结点多了一个孩子结点

      分析一下, 旋转导致哪些结点产生了变化, 由图可看到, 只有失衡结点的左子结点(结点15)和失衡结点(结点25)的边指向产生了变化, 其他结点都没有变化

      总不能无缘无故将新的根结点的右孩子(结点20)挂到其他结点下吧, 如果其他结点原来就有孩子结点, 那也没有位置可以挂, 所以只能将其挂为失衡结点(结点25)的左孩子

      左左失衡3.png

  3. 上图看的不够直观, 将其摆正
    左左失衡4.png

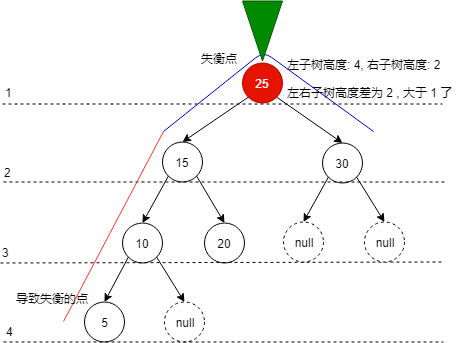
如何才能知道结点失衡了

给结点添加一个成员变量: 树的高度. 默认高度为 1

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private class 结点 {

    public 键 _键;

    public 值 _值;

    public 结点 _左子结点;

    public 结点 _右子结点;

    public int _树的高度;

    public 结点(键 _键, 值 _值, 结点 _左子结点, 结点 _右子结点) {
        this._键 = _键;
        this._值 = _值;
        this._左子结点 = _左子结点;
        this._右子结点 = _右子结点;
        this._树的高度 = 1;
    }
}

当递归添加结点时, 添加完后, 递归更新每个结点的高度

java
1
2
3
4
_树或子树的根结点._树的高度 = Math.max(
    _获取树的高度(_树或子树的根结点._左子结点),
    _获取树的高度(_树或子树的根结点._右子结点)
) + 1;

知道每个结点高度后, 只要拿当前结点的左右孩子结点的高度相减, 绝对值大于 1 ,则说明树失衡了

如何判断是哪一种失衡

添加时有两种方式判断是那一种失衡, 而删除时只能方式一

  • 方式一

    java
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    int _平衡因子 = _获取平衡因子(_树或子树的根结点);

    if(_平衡因子 < -1 && _获取平衡因子(_树或子树的根结点._右子结点) <= 0){ //右右失衡

        return _右右失衡_左旋(_树或子树的根结点);

    }else if(_平衡因子 < -1 && _获取平衡因子(_树或子树的根结点._右子结点) >= 0){ //右左失衡

        return _右左失衡_先右旋失衡结点的右子结点_再左旋失衡结点(_树或子树的根结点);

    } else if(_平衡因子 > 1 && _获取平衡因子(_树或子树的根结点._左子结点) >= 0){ //左左失衡

        return _左左失衡_右旋(_树或子树的根结点);

    }else if(_平衡因子 > 1  &&  _获取平衡因子(_树或子树的根结点._左子结点) <= 0) { //左右失衡

        return _左右失衡_先左旋失衡结点左子结点_再右旋失衡结点(_树或子树的根结点);

    }

  • 方式二

    java
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    int _平衡因子 = _获取平衡因子(_树或子树的根结点);

            if(_平衡因子 < -1 && _键.compareTo(_树或子树的根结点._右子结点._键) > 0){ //右右失衡

                return _右右失衡_左旋(_树或子树的根结点);

            }else if(_平衡因子 < -1 && _键.compareTo(_树或子树的根结点._右子结点._键) < 0){ //右左失衡

                return _右左失衡_先右旋失衡结点的右子结点_再左旋失衡结点(_树或子树的根结点);

            } else if(_平衡因子 > 1 && _键.compareTo(_树或子树的根结点._左子结点._键) < 0){ //左左失衡

                return _左左失衡_右旋(_树或子树的根结点);

            }else if(_平衡因子 > 1  && _键.compareTo(_树或子树的根结点._左子结点._键) > 0) { //左右失衡

                return _左右失衡_先左旋失衡结点左子结点_再右旋失衡结点(_树或子树的根结点);

            }

代码实现

代码和普通二叉树的实现几乎一样, 除了递归添加和递归删除结点后, 要递归更新树的高度, 然后递归判断结点是否失衡以及是那一种失衡, 然后通过”旋转”算法调整失衡的结点

旋转算法如下

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
private  int _获取树的高度(结点 _树或子树根结点){
    //如果树是空，那么高度也就是0
    return _树或子树根结点 == null ? 0 : _树或子树根结点._树的高度;
}

private  int _获取平衡因子(结点 _树或子树根结点){
    //如果高度小于等于1，那么就是一个只有根节点或空树，是平衡树。
    if(_获取树的高度(_树或子树根结点) <= 1){
        return 0;
    }

    //计算左右子树高度差，绝对值小于等于1的就是平衡树
    return _获取树的高度(_树或子树根结点._左子结点) - _获取树的高度(_树或子树根结点._右子结点);
}

private 结点 _左左失衡_右旋(结点 _结点){

    结点 _旋转后的新根结点;

    _旋转后的新根结点 = _结点._左子结点;

    _结点._左子结点 =_旋转后的新根结点._右子结点;
    _旋转后的新根结点._右子结点 = _结点;

    _结点._树的高度 = Math.max(_获取树的高度(_结点._左子结点), _获取树的高度(_结点._右子结点))+1;
    _旋转后的新根结点._树的高度 = Math.max(_获取树的高度(_旋转后的新根结点._左子结点), _获取树的高度(_旋转后的新根结点._右子结点))+1;

    return _旋转后的新根结点;
}

private 结点 _右右失衡_左旋(结点 _结点){

    结点 _旋转后的新根结点;

    _旋转后的新根结点 = _结点._右子结点;

    _结点._右子结点 = _旋转后的新根结点._左子结点;
    _旋转后的新根结点._左子结点 = _结点;


    _结点._树的高度 = Math.max(_获取树的高度(_结点._左子结点), _获取树的高度(_结点._右子结点))+1;
    _旋转后的新根结点._树的高度 = Math.max(_获取树的高度(_旋转后的新根结点._左子结点), _获取树的高度(_旋转后的新根结点._右子结点))+1;

    return _旋转后的新根结点;
}

private 结点 _左右失衡_先左旋失衡结点左子结点_再右旋失衡结点(结点 _失衡结点){

    结点 _旋转后的新根结点;

    _失衡结点._左子结点 = _右右失衡_左旋(_失衡结点._左子结点);

    _旋转后的新根结点 = _左左失衡_右旋(_失衡结点);

    return _旋转后的新根结点;
}

private 结点 _右左失衡_先右旋失衡结点的右子结点_再左旋失衡结点(结点 _失衡结点){

    结点 _旋转后的新根结点;

    _失衡结点._右子结点 = _左左失衡_右旋(_失衡结点._右子结点);

    _旋转后的新根结点 = _右右失衡_左旋(_失衡结点);

    return _旋转后的新根结点;
}

添加结点代码如下

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
private 结点 _新添(结点 _树或子树的根结点, 键 _键, 值 _值) {

    //如果指定的树为空
    if (_树或子树的根结点 == null){
        _结点个数++;
        return new 结点(_键,_值, null,null);
    }

    //指定的树不空, 比较 新结点的键 和 指定树的根结点的键
    int _比较结果 = _键.compareTo(_树或子树的根结点._键);

    if (_比较结果 > 0){ //新结点的键 大于 指定数根节点的键

        _树或子树的根结点._右子结点 = _新添(_树或子树的根结点._右子结点,_键,_值); //递归放在右子树

    }else if(_比较结果 < 0){ //新结点的键 大于 指定数根节点的键

        _树或子树的根结点._左子结点 = _新添(_树或子树的根结点._左子结点,_键,_值);//递归放在左子树

    }else{ //新结点的键 等于 指定树根节点的键

        _树或子树的根结点._值 = _值; //则替换指定子树根结点的值为新的值

        return _树或子树的根结点;

    }

    _树或子树的根结点._树的高度 = Math.max(_获取树的高度(_树或子树的根结点._左子结点), _获取树的高度(_树或子树的根结点._右子结点))+1;

    int _平衡因子 = _获取平衡因子(_树或子树的根结点);

    if(_平衡因子 < -1 && _键.compareTo(_树或子树的根结点._右子结点._键) > 0){ //右右失衡

        return _右右失衡_左旋(_树或子树的根结点);

    }else if(_平衡因子 < -1 && _键.compareTo(_树或子树的根结点._右子结点._键) < 0){ //右左失衡

        return _右左失衡_先右旋失衡结点的右子结点_再左旋失衡结点(_树或子树的根结点);

    } else if(_平衡因子 > 1 && _键.compareTo(_树或子树的根结点._左子结点._键) < 0){ //左左失衡

        return _左左失衡_右旋(_树或子树的根结点);

    }else if(_平衡因子 > 1  && _键.compareTo(_树或子树的根结点._左子结点._键) > 0) { //左右失衡

        return _左右失衡_先左旋失衡结点左子结点_再右旋失衡结点(_树或子树的根结点);

    }

    return _树或子树的根结点;
}

删除结点代码如下

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
private 结点 _删除(结点 _树或子树的根结点, 键 _键) {

    if (_树或子树的根结点 == null){
        return null; //找完所有节点都没找到
    }


    int _比较结果 = _键.compareTo(_树或子树的根结点._键);
    if (_比较结果 > 0){

        _树或子树的根结点._右子结点 = _删除(_树或子树的根结点._右子结点,_键);//递归从右子树找

    }else if(_比较结果 < 0){

        _树或子树的根结点._左子结点 = _删除(_树或子树的根结点._左子结点,_键);//递归从左子树找

    }else{ // _比较结果 == 0 找到了

        //让 结点个数-1
        _结点个数--;


        // 情况一 没有右子树 拿左子树补位
        if (_树或子树的根结点._右子结点 == null){
            return _树或子树的根结点._左子结点;
        }

        // 情况二 没有左子树 拿右子树补位
        if (_树或子树的根结点._左子结点 == null){
            return _树或子树的根结点._右子结点;
        }


        // 情况三 既有右子树又有左子树 从右子树中找到一个最小键来 补位 被删除的结点

        // 右子树中的最小键结点就是右子树中: 最左下侧的结点 或 右子树的根节点, 找到它并删除它

        结点 _右子树中键最小的结点 = _树或子树的根结点._右子结点;
        结点 _右子树中键最小的结点的双亲节点 = _树或子树的根结点._右子结点;
        while(_右子树中键最小的结点的双亲节点._左子结点 != null){

            if (_右子树中键最小的结点的双亲节点._左子结点._左子结点 == null){ //找到最小键结点的双亲结点了

                _右子树中键最小的结点 = _右子树中键最小的结点的双亲节点._左子结点; //保存下来

                _右子树中键最小的结点的双亲节点._左子结点 = null; // 使双亲结点的左子结点指向空

            }else{

                _右子树中键最小的结点的双亲节点 = _右子树中键最小的结点的双亲节点._左子结点;

            }

        }

        // 更新指针指向

        _右子树中键最小的结点._左子结点 = _树或子树的根结点._左子结点;

        _右子树中键最小的结点._右子结点 = _树或子树的根结点._右子结点;

        _树或子树的根结点 = _右子树中键最小的结点;

    }

    _树或子树的根结点._树的高度 = Math.max(_获取树的高度(_树或子树的根结点._左子结点), _获取树的高度(_树或子树的根结点._右子结点))+1;

    int _平衡因子 = _获取平衡因子(_树或子树的根结点);

    if(_平衡因子 < -1 && _获取平衡因子(_树或子树的根结点._右子结点) <= 0){ //右右失衡

        return _右右失衡_左旋(_树或子树的根结点);

    }else if(_平衡因子 < -1 && _获取平衡因子(_树或子树的根结点._右子结点) >= 0){ //右左失衡

        return _右左失衡_先右旋失衡结点的右子结点_再左旋失衡结点(_树或子树的根结点);

    } else if(_平衡因子 > 1 && _获取平衡因子(_树或子树的根结点._左子结点) >= 0){ //左左失衡

        return _左左失衡_右旋(_树或子树的根结点);

    }else if(_平衡因子 > 1  &&  _获取平衡因子(_树或子树的根结点._左子结点) <= 0) { //左右失衡

        return _左右失衡_先左旋失衡结点左子结点_再右旋失衡结点(_树或子树的根结点);

    }

    return _树或子树的根结点;
}
文章作者: Juchia Lu
文章链接: https://juchia.com/2018/12/05/%E4%BA%8C%E5%8F%89%E5%B9%B3%E8%A1%A1%E6%A0%91%E7%9A%84%E6%97%8B%E8%BD%AC%E9%97%AE%E9%A2%98/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Juchia！
算法和数据结果 树 二叉树 二叉平衡树
相关推荐
2018-12-06
二叉平衡树旋转问题的全部情况图示
2018-11-26
二叉查找树的定义和存储结构
2018-11-22
二叉树的存储结构
2018-11-21
二叉树以及完全二叉树的性质
2018-11-20
二叉树的定义和特点以及术语
2018-11-20
树的存储结构
简