二叉树的存储结构

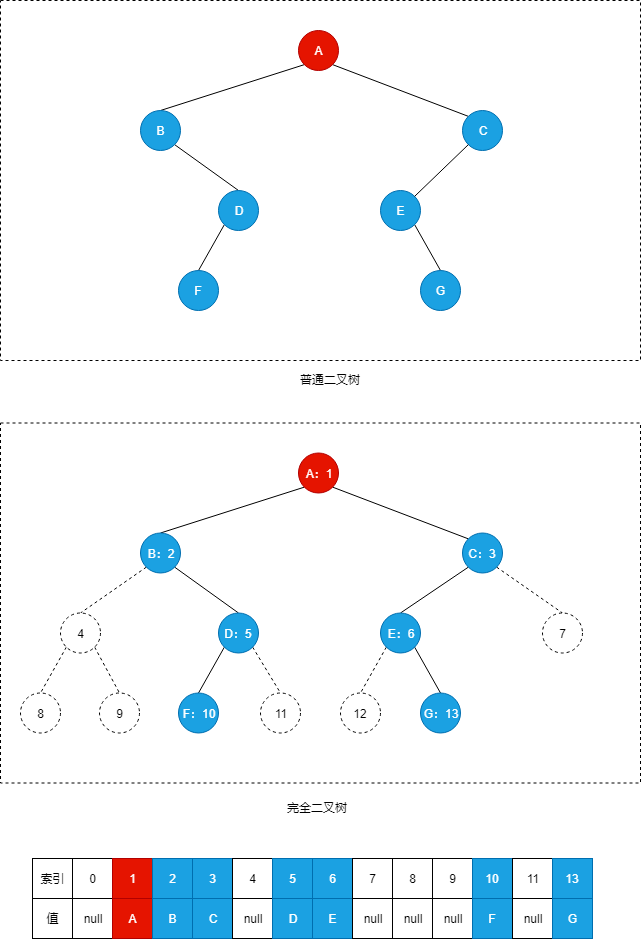
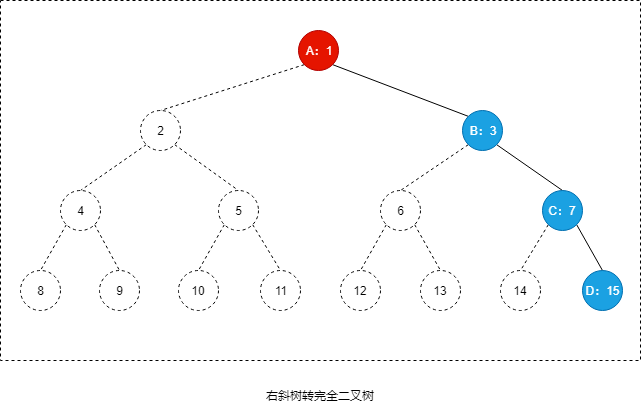
顺序存储

根据完全二叉树的性质：

结点 i 的的双亲结点为向下取整(i/2)
结点 i 的左孩子为 2i
结点 i 的右孩子为 2i+1

所以完全二叉树可以很容易的确定结点间的关系，如找双亲，找左子节点，找右子节点，找兄弟节点

因此可以将一颗普通二叉树转换成完全二叉树用一维数组来储存

优点
查操操作简单，增删操作也简单，因为已经用 null 占位了，不用挪位置
缺点
浪费存储空间，最坏情况是右斜树，只需要 k 个空间，却分配 2^k - 1 个空间

所以一般用来存完全二叉树

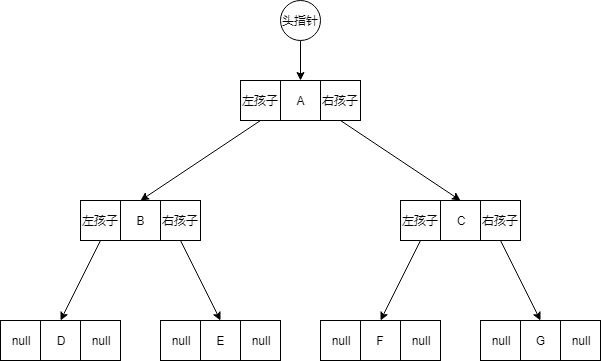
二叉链表存储

特点
采用链表实现
优点
找孩子结点容易
缺点
1. 找父结点困难（从根结点遍历，看哪个结点的孩子结点等于要找的结点）
2. 找兄弟节点困难（先找父节点）

数据结构

java

public class 结点{
 Object data; //数据
 结点 leftChild; //指向左孩子结点
 结点 rightChild; //指向右孩子结点
}

图示

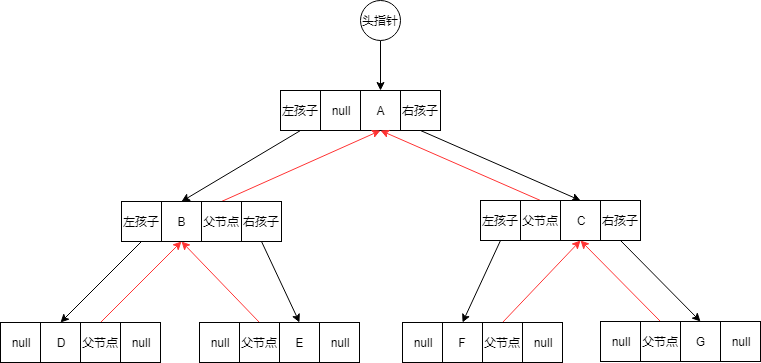
三叉链表存储

特点
采用链表实现
优点
找孩子和双亲结点都容易
缺点
占用空间变大了

数据结构

java

public class 结点{
 Object data; //数据
 结点 parent; //指向双亲结点
 结点 leftChild; //指向左孩子结点
 结点 rightChild; //指向右孩子结点
}

图示

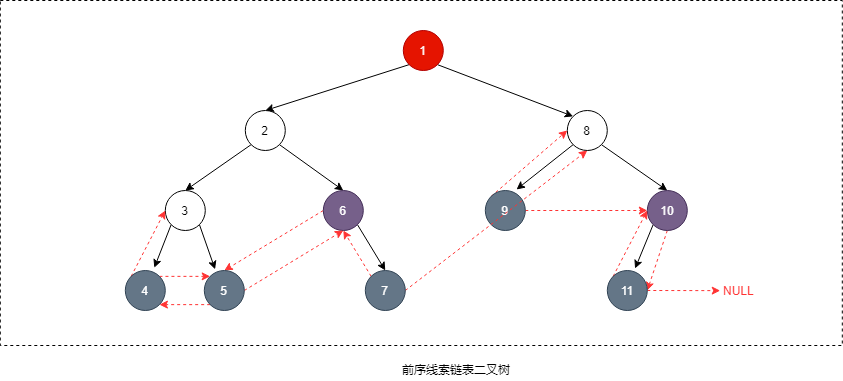
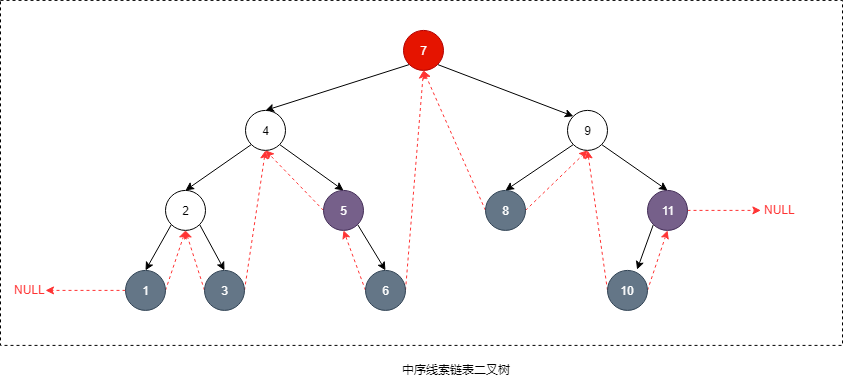
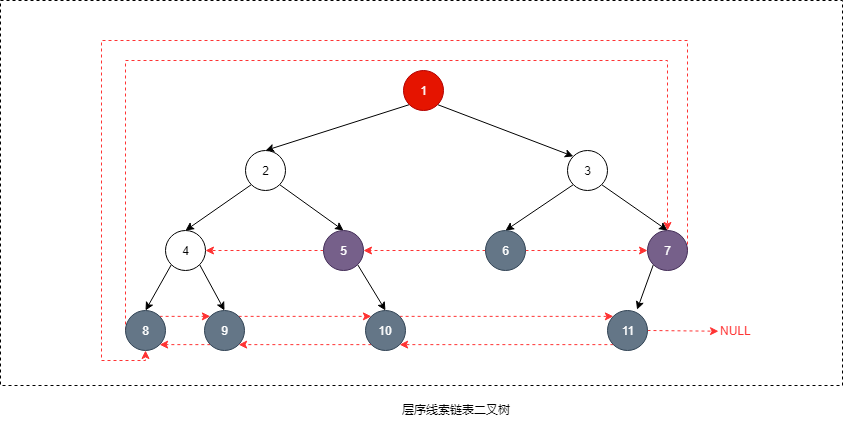
线索链表存储

二叉树是非线性结构，但二叉树按某种顺序遍历时经过的结点却是线性的。想很快找到遍历顺序中某一结点的前驱或后继，但又不想每次都得对二叉树再遍历一遍，这就需要把结点的前驱和后继信息记录下来。在 n 个节点的二叉树中，有 2n 个指针域，但是只有 2n-1 个用来存左孩子或右孩子，还有 2n + 1 个是 null，可以将这些空的指针域用来存这部分的结点按遍历顺序时的前驱结点或后继结点

特点
采用链表实现, 可以存储前序、中序、后序、层序任一种遍历时的这部分结点前继结点或后继结点
优点
1. 找孩子容易
2. 可以很容易访问这部分结点的前驱结点或后继结点
3. 利用中序线索二叉树进行中序遍历时，不必采用递归，速度比一般二叉树的遍历速度快，节约运行内存
缺点
1. 占用空间变大
2. 结点的插入和删除麻烦，且速度也较慢
3. 并没有让每一个节点都能访问到他的前驱和后继

数据结构

java

public class 结点{
 Object data; //数据
 结点 leftChildOrBefore; //指向左孩子结点或前驱结点
 结点 rightChildOrAfter; //指向右孩子结点或后继结点
 boolean isBefore; //leftChildOrBefore 存的是否是前驱结点
 boolean isAfter; //rightChildOrAfter 存的是否是后继结点
}

图示
- 前序线索链表二叉树
- 中序线索链表二叉树
- 后序线索链表二叉树
- 层序线索链表二叉树