二叉树以及完全二叉树的性质

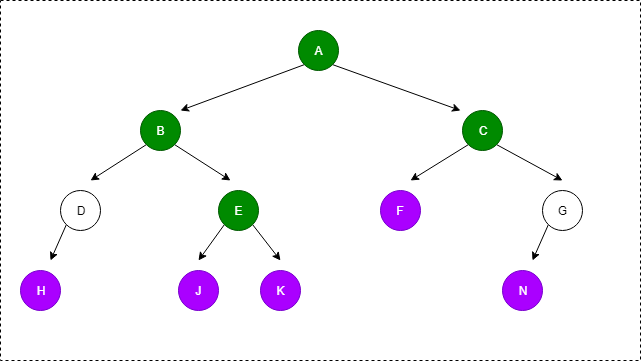
二叉树的性质

（一）第 i 层 最多有 2^i-1 个结点

证明：略

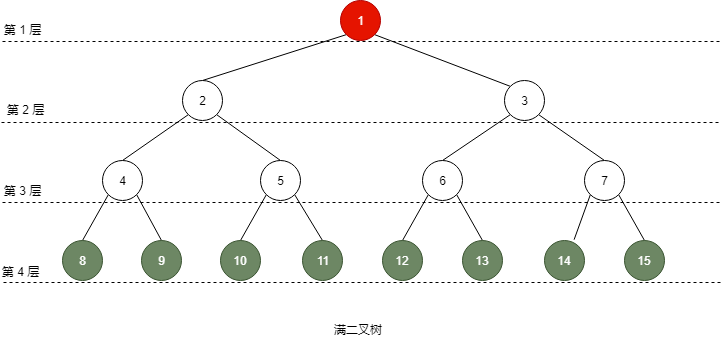
（二）深度为 k 的二叉树，至多 2^k - 1 个结点，至少 k 个结点

至多：满二叉树时

证明：略

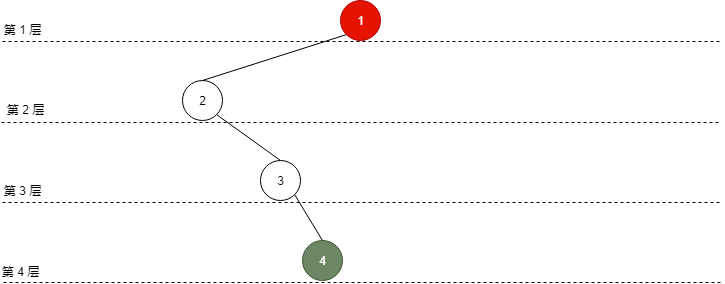
至少：每层只有一个结点

证明：略

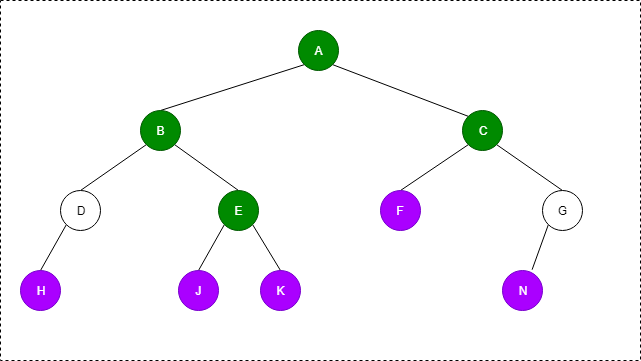
（三）度为0的结点个数（叶子结点数） = 度为2的结点个数 + 1

证明：

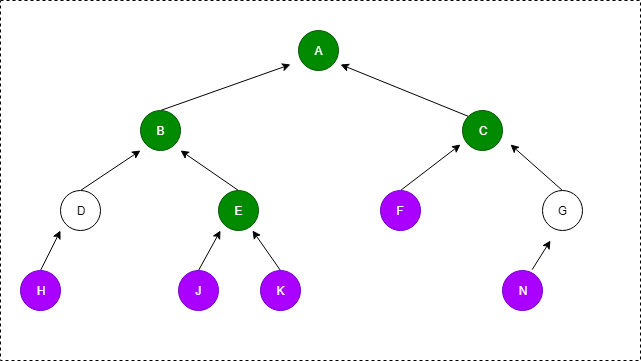
除了根结点，每个结点都有一个分支指向父结点： 结点数 = 分支数 + 1 ①

反过来，这些分支也可以看作是度是1的结点和度是2的结点射出的
所以：分支数 = 度为1的结点数 + 2*度为2的结点数 ②

由： 结点数 = 分支数 + 1 ① 和 分支数 = 度为1的结点数 + 2*度为2的结点数 ②
得：结点数 = 度为1的结点数 + 2*度为2的结点数 + 1 ③

再：结点数 = 度为1的结点数 + 2*度为2的结点数 + 1 ③ 和 结点数 = 度为1的结点数 + 度为2的结点数 + 度为0的结点数
得：度为0的结点数 = 度为2的结点数 + 1

（四）包含 n 个结点的二叉树的高度至少为 log₂(n+1)。

证明：根据”性质二”可知，高度为 k 的二叉树最多有结点 n = 2^k - 1 个。反之，对于包含 n 个节点的二叉树的高度至少为 k = log2(n+1)。

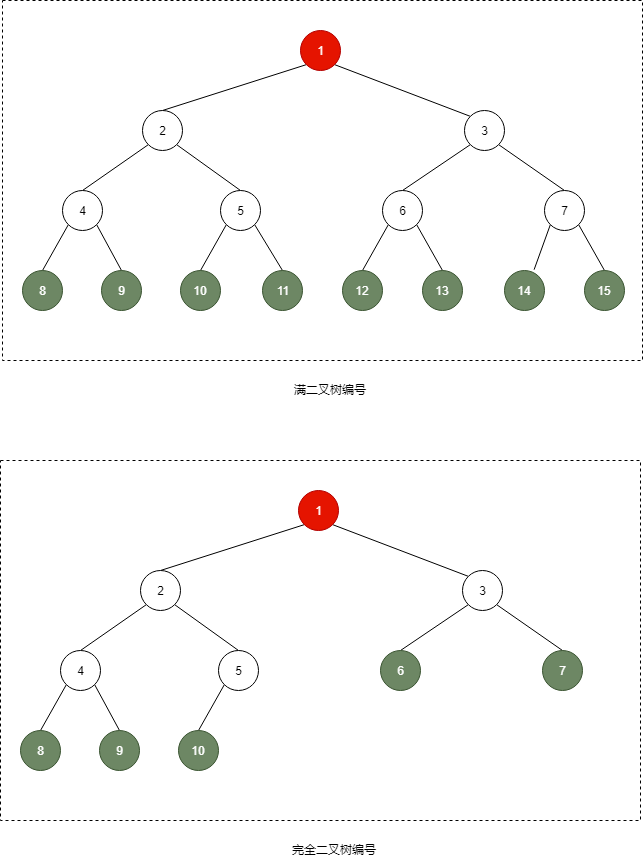
完全二叉树的性质

（一）具有 n 个结点得完全二叉树的深度为： 向下取整(log₂n) + 1

（二）将 n 个节点的完全二叉树各结点按层序编号, 结点 i 有以下性质：

• 如果 i=1，i 为根结点，无双亲；如果 i>1，它的双亲结点为 向下取整(i/2)
• 如果 2i<=n，结点 i 的左孩子为 2i；否则无左孩子
• 如果 2i+1<=n，结点 i 的右孩子为 2i+1；否则无右孩子
• 结点 i 所在的层次为 向下取整(log₂i) + 1
• i 为奇数，且 i!=1，i 处于右兄弟的位置，它的左兄弟为 i-1
• i 为偶数，且 i!=n，i 处于左兄弟的位置，它的右兄弟为 i+1