快速排序 | Juchia

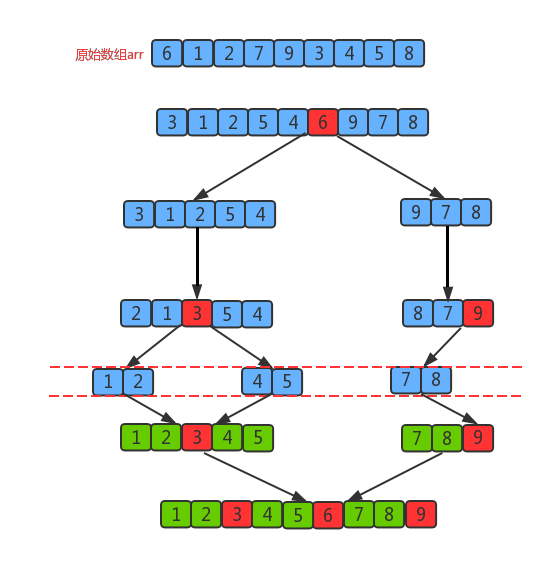
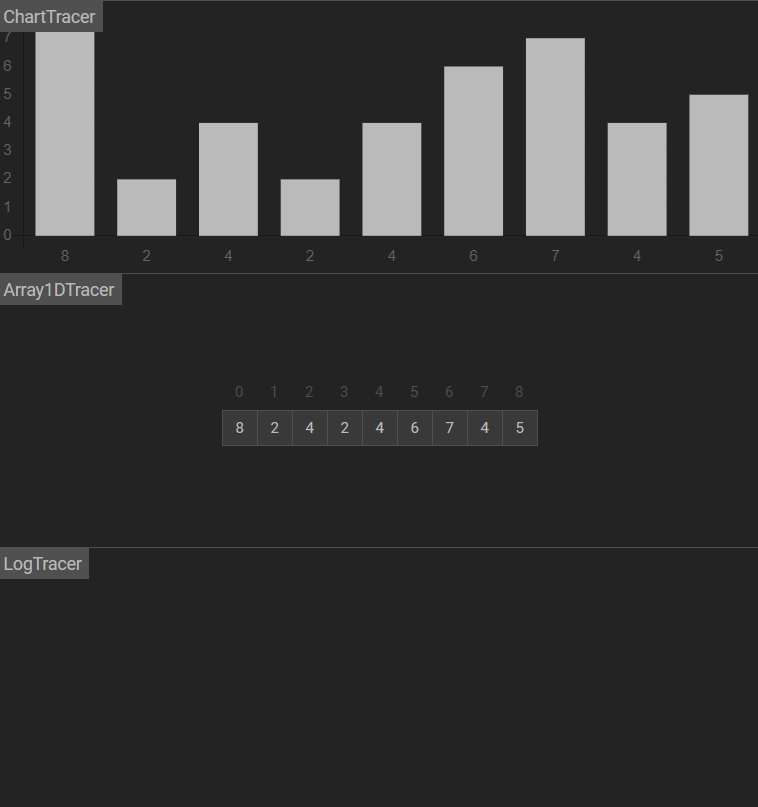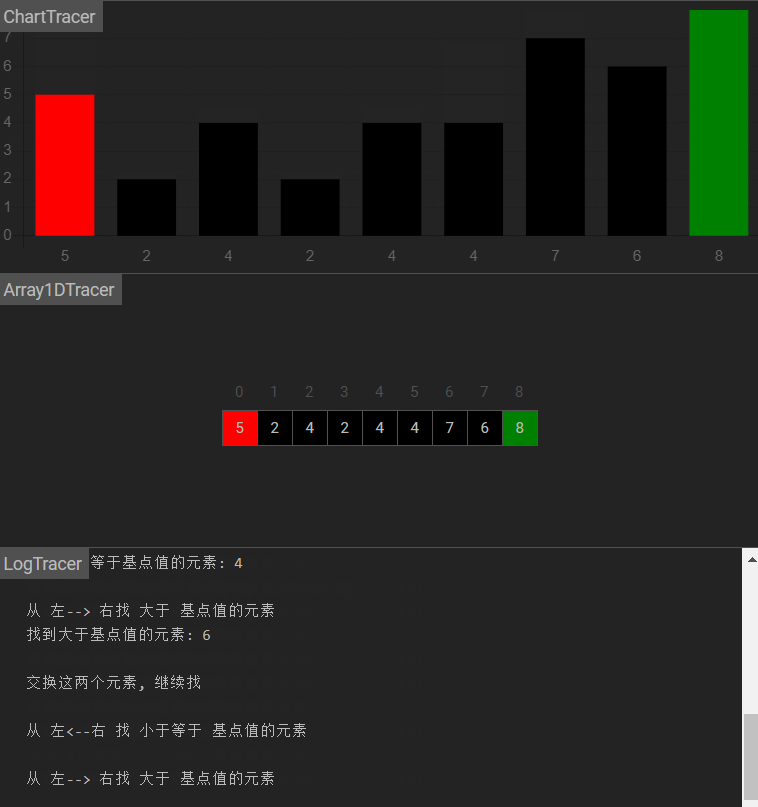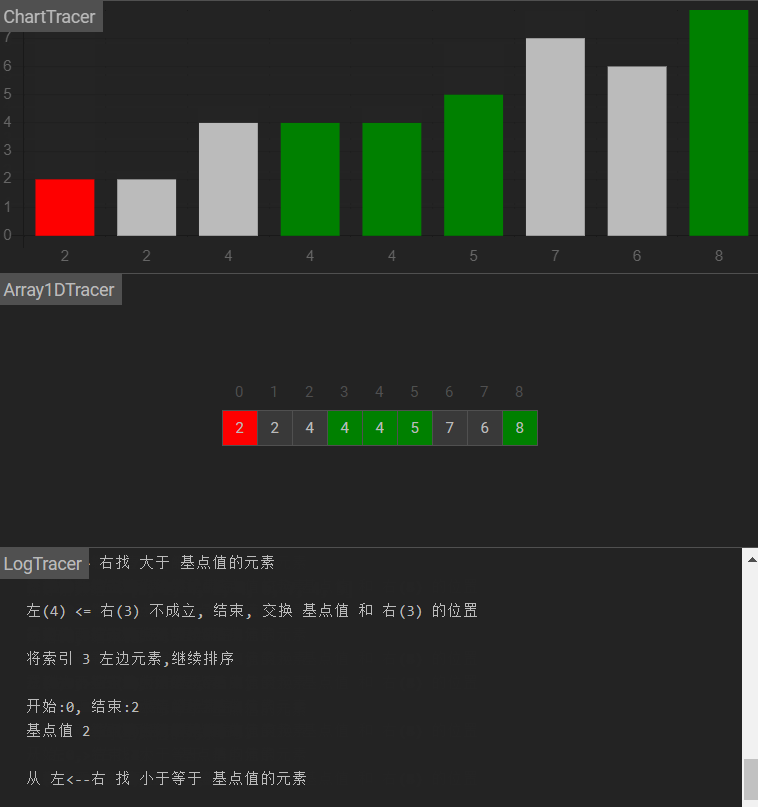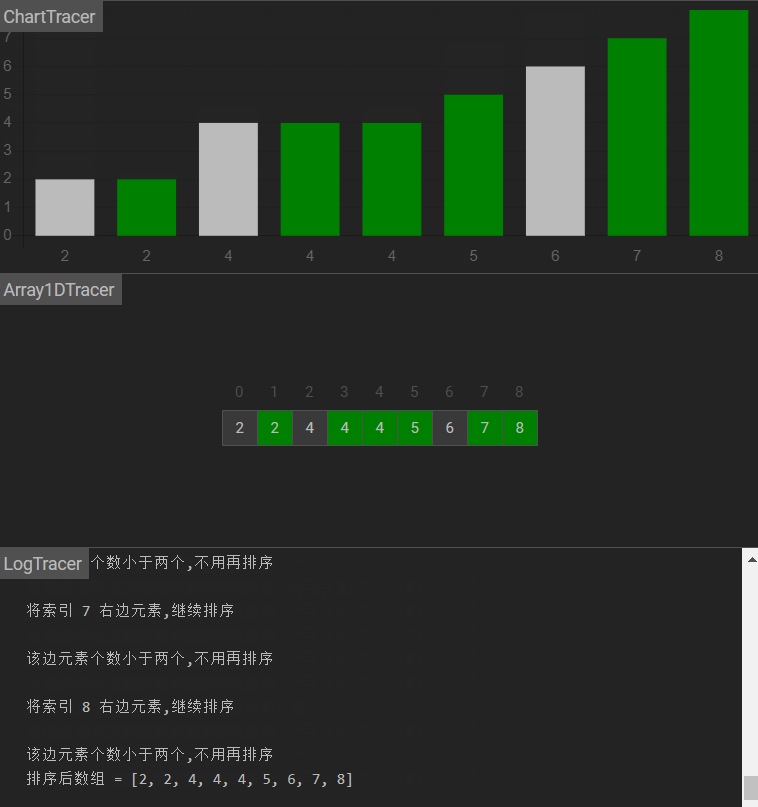
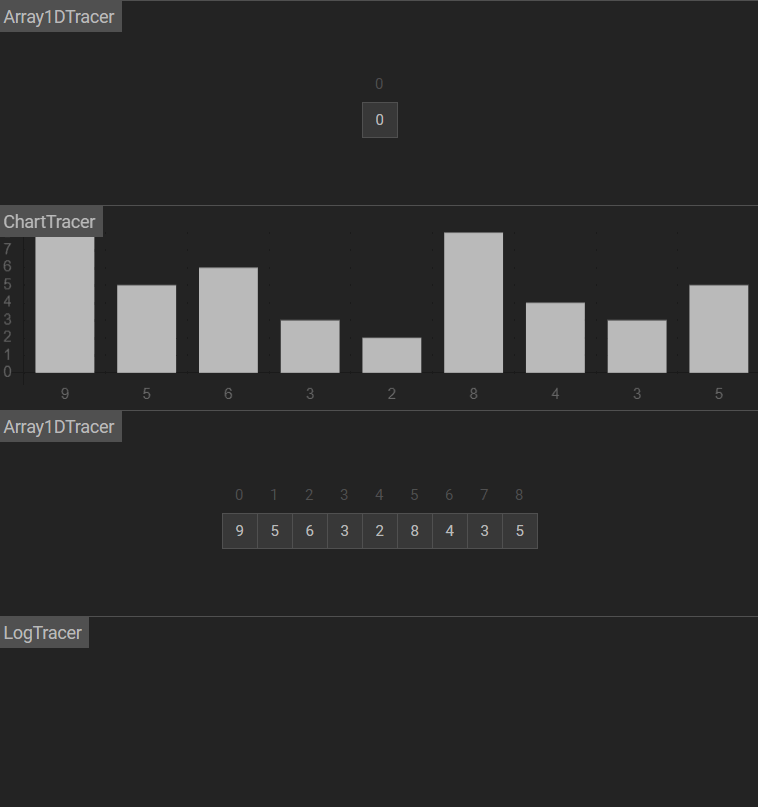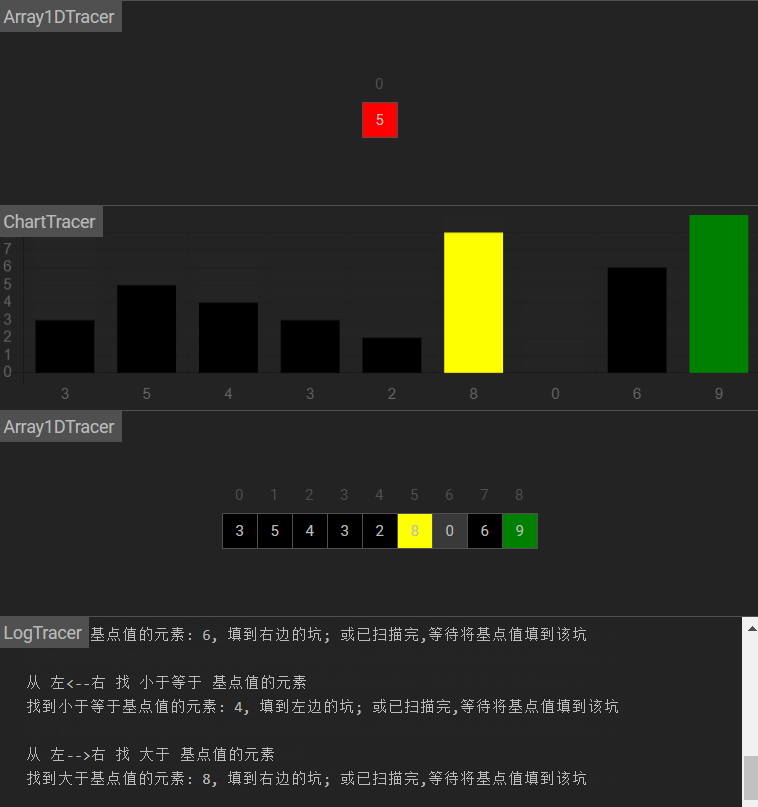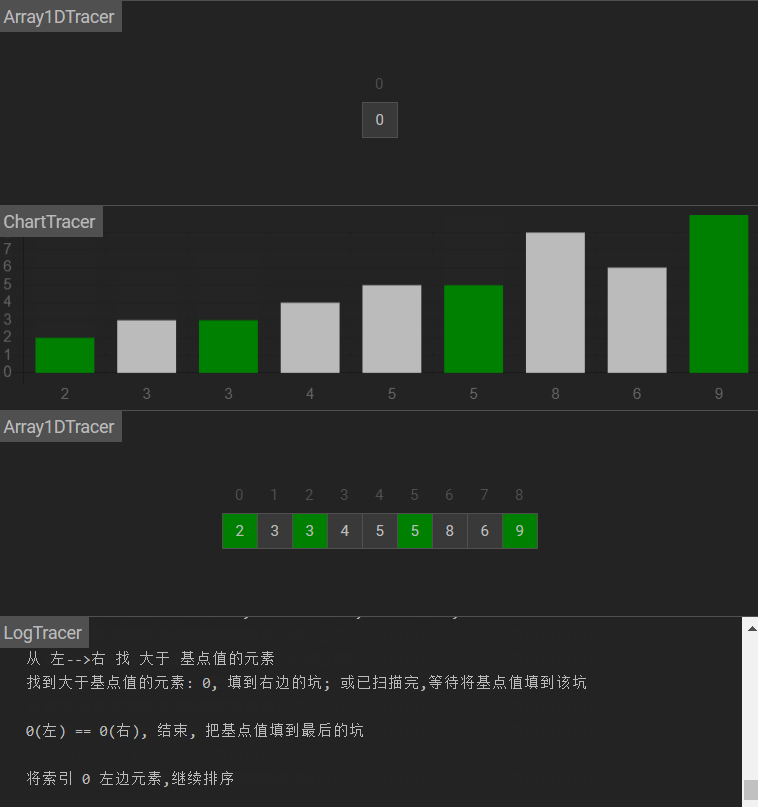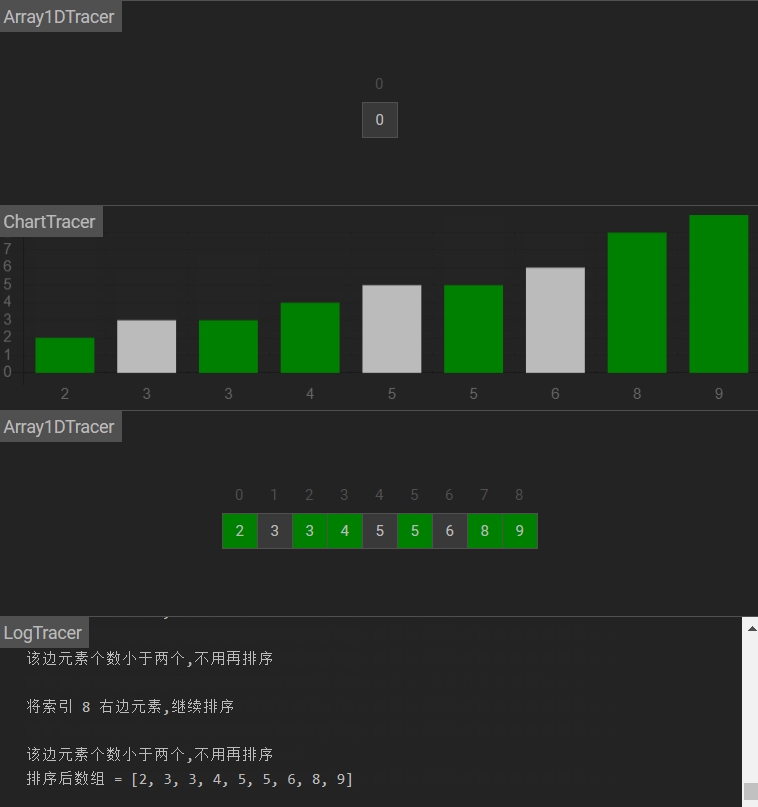
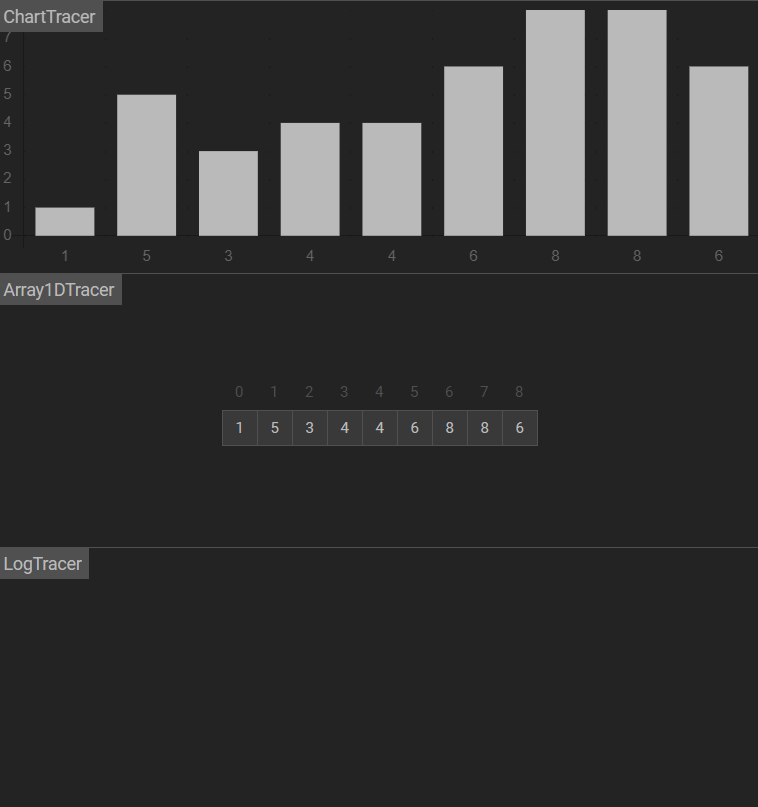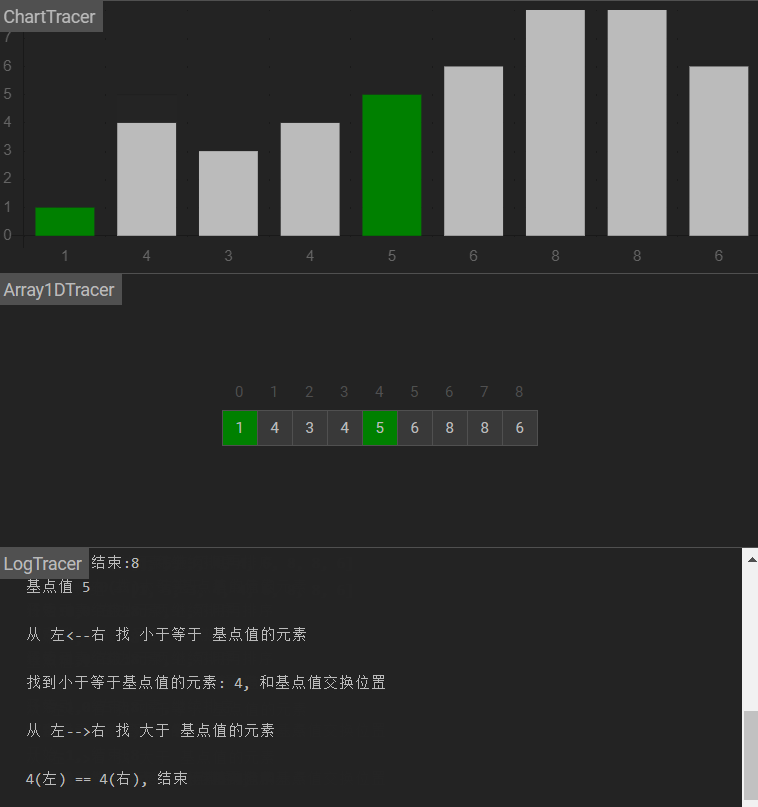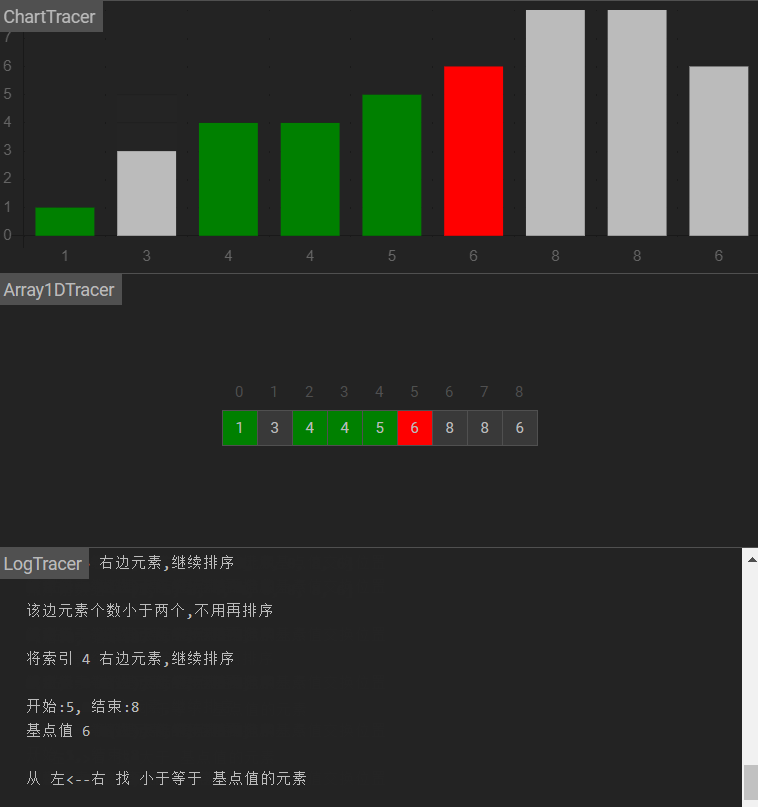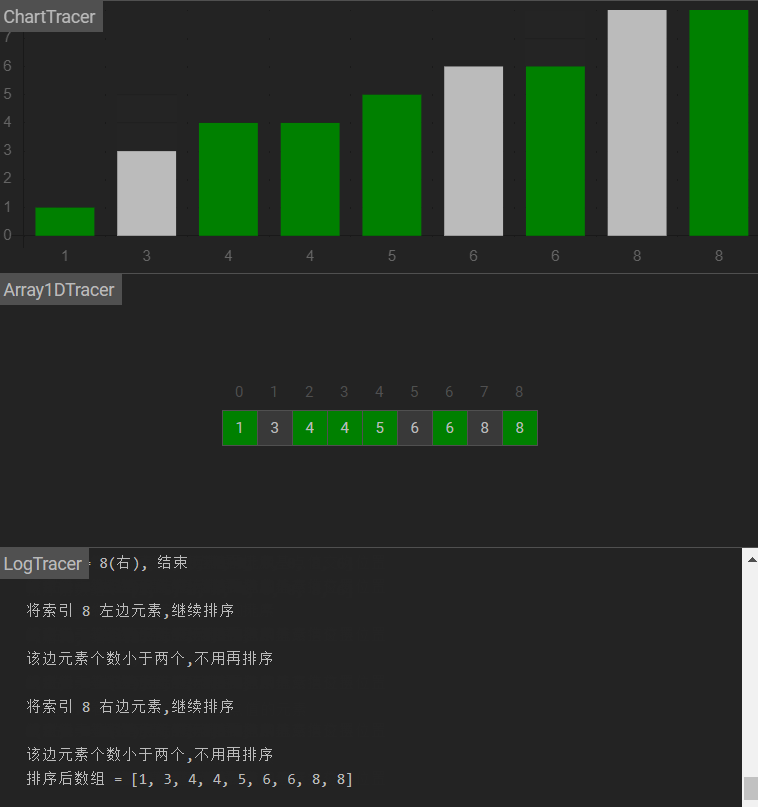
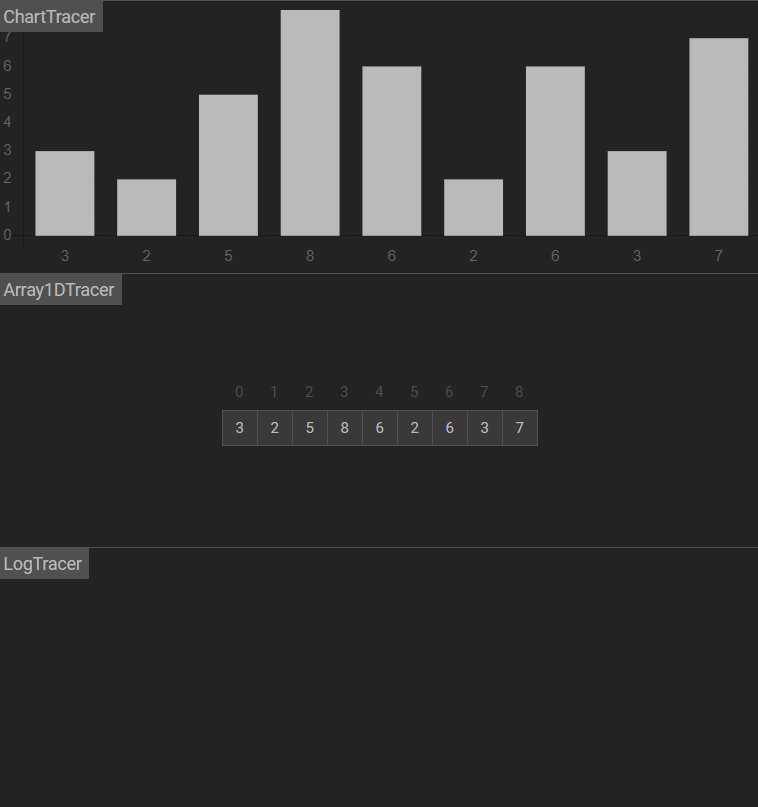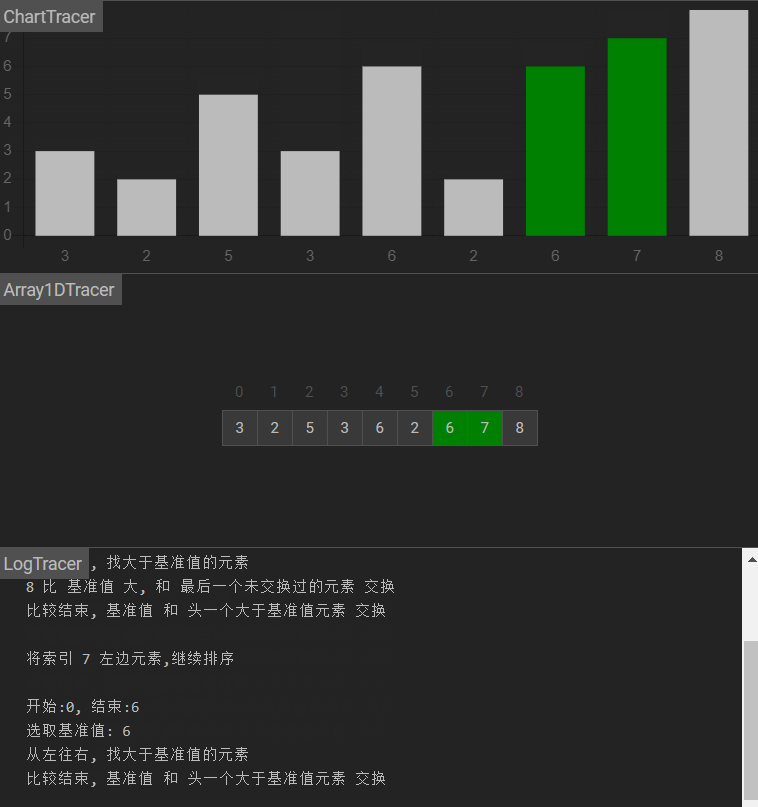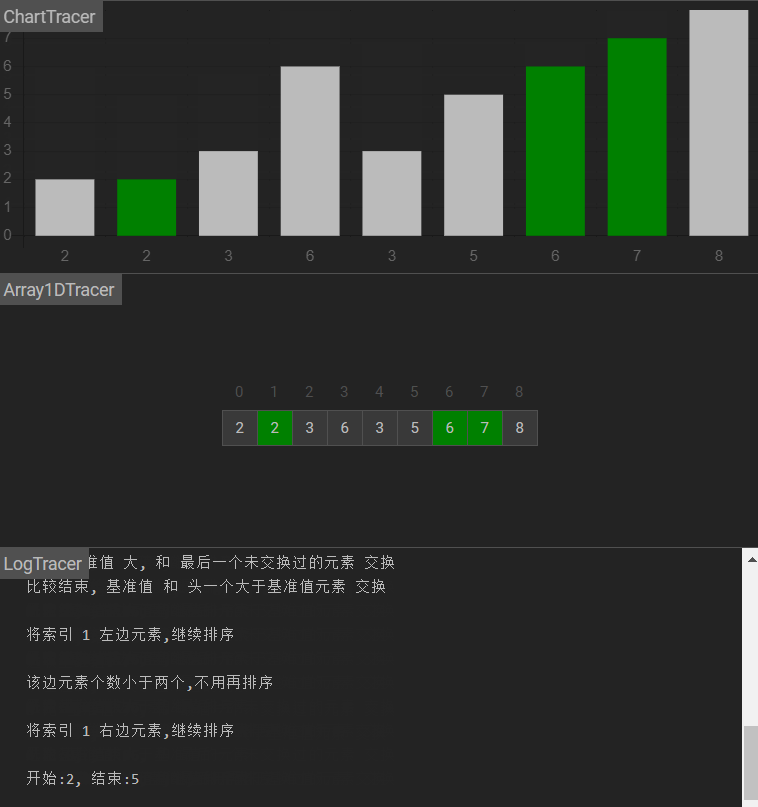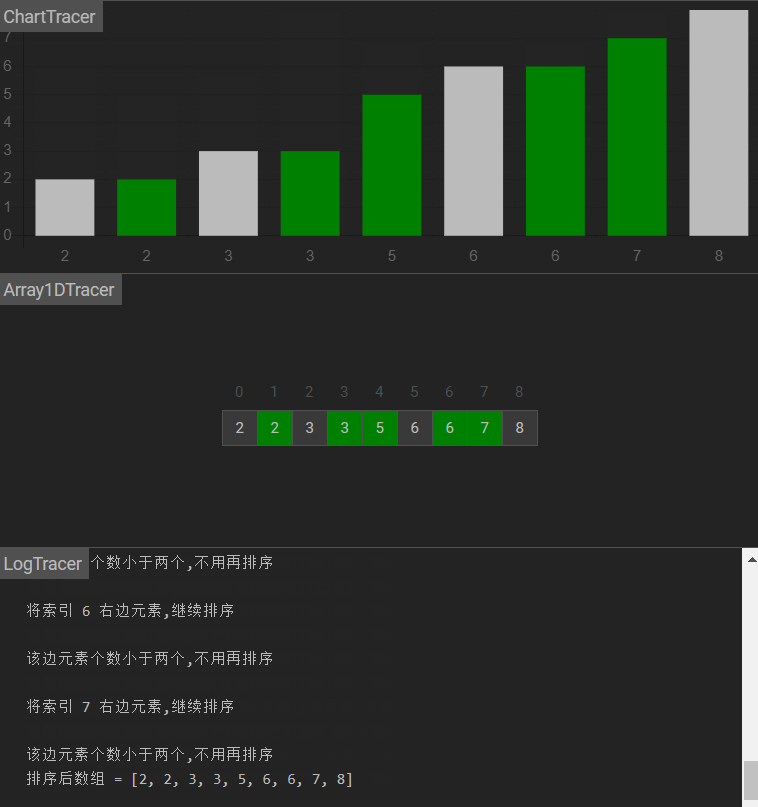
图示

基本原理

两边扫描交换法
两边扫描填坑法之基点元素暂存
两边扫描填坑法之基点元素每次交换
单边扫描法

原理

Code

1.首先设定一个分界值，通过该分界值将数组分成左右两部分； 
2.将大于分界值的数据放到到数组右边，小于或等于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于分界值；
3.然后，左边和右边的数据又可以独立排序，重复1和2步骤；
4.重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了

实现

通用函数

java

public static void _排序(Comparable[] a) {
    _排序(a, 0, a.length-1);
}


public static void _排序(Comparable[] a, int _开始, int _结束) {

    if(_结束 < _开始){ // 只有一个元素时, 如索引为1, 那么 (1,1-1)=(1,0), (1+1,1)=(2,1)
        return;
    }

    int _基点位置 = _下面的四种核心算法(a, _开始, _结束);

    _排序(a, _开始,_基点位置-1);
    _排序(a, _基点位置+1, _结束);

}

两边扫描交换法

java

public static int _两边扫描交换法(Comparable[] a, int _开始, int _结束) {

    //定义两个指针，分别指向待最小索引处和最大索引处

    // 为什么 _左边遍历索引 可以从 _开始+1 开始 ?
    // 答: while 判断条件由 不等于 变成 小于等于即可
    //     比如 0 1 2 3 4, 从右往左找小于等于基准值时,
    //     扫到 1 (_左边遍历索引 <= _右边遍历索引) 1<=1 所以 会进去while循环
    //	   直到 左边(1) <= 右边(0) 不成立, 退出循环
    int _左边遍历索引 = _开始+1;
    int _右边遍历索引 = _结束;

    //选取基点 
    Comparable _基点值 = a[_开始];

    while(_左边遍历索引 <= _右边遍历索引){

        //先 从右往左， 找一个小于等于基点值的元素
        while(_左边遍历索引 <= _右边遍历索引 && _是否不小于等于(a[_右边遍历索引], _基点值)){
            _右边遍历索引--;
        }

        //再 从左往右 找到一个大于基点值的元素
        while(_左边遍历索引 <= _右边遍历索引 && _是否不大于(a[_左边遍历索引], _基点值)){
            _左边遍历索引++;
        }

        if (_左边遍历索引 <= _右边遍历索引){
            _交换(a,_左边遍历索引,_右边遍历索引);
        } else {
            _交换(a,_开始,_右边遍历索引);
            break;
        }
    }
    return _右边遍历索引;
}

两边扫描填坑法之基点元素暂存

java

public static int _两边扫描填坑法之基点元素暂存(Comparable[] a, int _开始, int _结束) {

    int _左边遍历索引 = _开始;
    int _右边遍历索引 = _结束;

    //选取基点, 
    Comparable _基点值 = a[_开始];

    while(_左边遍历索引 != _右边遍历索引){

        //先从 左<--右， 找一个 小于等于 基点值的元素
        while(_左边遍历索引 != _右边遍历索引 && _是否不小于等于(a[_右边遍历索引], _基点值)){
            _右边遍历索引--;
        }
        //把找到的元素填到左边的坑
        a[_左边遍历索引] = a[_右边遍历索引];

        //再从 左-->右 找到一个 大于 基点值的元素
        while(_左边遍历索引 != _右边遍历索引 && _是否不大于(a[_左边遍历索引], _基点值)){
            _左边遍历索引++;
        }
        //把找到的元素填到右边的坑
        a[_右边遍历索引] = a[_左边遍历索引];

        if (_左边遍历索引 == _右边遍历索引){
            //最后把基点值填到坑
            a[_右边遍历索引] = _基点值;
            break;
        }
    }
    return _右边遍历索引;
}

两边扫描填坑法之基点元素每次交换

java

public static int 两边扫描填坑法之基点元素没次交换(Comparable[] a, int _开始, int _结束) {

    int _左边遍历索引 = _开始;
    int _右边遍历索引 = _结束;

    //选取基点
    Comparable _基点值 = a[_开始];

    while(_左边遍历索引 != _右边遍历索引){

        //先从 左<--右 ， 找一个 小于等于 基点值的元素
        while(_左边遍历索引 != _右边遍历索引){
            if( _是否小于等于(a[_右边遍历索引], _基点值)){
                _交换(a,_右边遍历索引,_左边遍历索引);
                //右边的元素刚刚交换到左边, 左边元素一定是小于等于基准值的
                //左边找大的元素可以跳过这个元素
                _左边遍历索引++; 
                break;
            }
            _右边遍历索引--;
        }

        //再 从左-->右 找到一个 大于 基点值的元素
        while(_左边遍历索引 != _右边遍历索引){
            if( _是否大于(a[_左边遍历索引], _基点值)){
                _交换(a,_左边遍历索引,_右边遍历索引);
                //左边的元素刚刚交换到右边, 右边元素一定是大于基准值的
                //左边找小于等于的元素可以跳过这个元素
                _右边遍历索引--;
                break;
            }
            _左边遍历索引++;
        }

    }
    return _右边遍历索引;
}

单边扫描法

java

//大于基准值的往后甩, 最后基准值和从左到右第一个大于它的元素交换
public static int _单边扫描法(Comparable[] a, int _开始, int _结束) {

    int _基准值索引 = _结束;

    for (int i = _开始; i < _结束; i++){
        if (_是否大于(a[i] , a[_基准值索引])) {
            //最后一个是基点值, 结束--后, 才是本轮的最后一个元素, 且交换过后就不用再比较了
            _结束--;
            _交换(a, i, _结束);
            // 而i--的保证了交换元素后下一次循环依旧使用当前位置的元素与基准值进行比较
            // 因为刚刚交换过来的元素还未与基准值比较过
            i--; 
        }
    }

    //最后一个大于基准值的元素(从左到右第一个) 和 基准值  交换
    _交换(a,_结束, _基准值索引); 

    return _结束;
}

性能

快速排序的一次切分从两头开始交替搜索，直到left和right重合，因此，一次切分算法的时间复杂度为O(n)，但整个快速排序的时间复杂度和切分的次数相关。

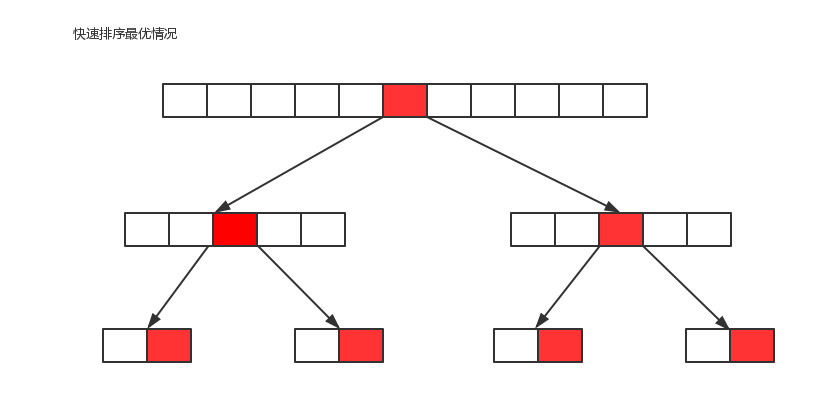
最好情况
每一次切分选择的基准数字刚好将当前序列等分

如果我们把数组的切分看做是一个树，那么上图就是它的优情况的图示，共切分了logn次，所以，优情况下快速排序的时间复杂度为O(nlogn)；
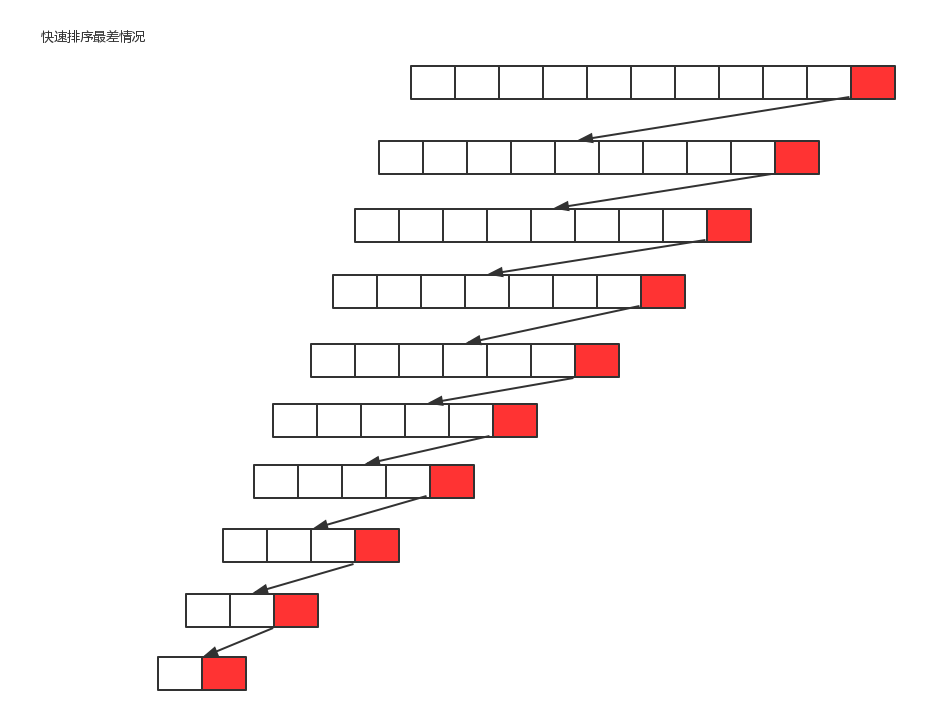
最坏情况
每一次切分选择的基准数字是当前序列中大数或者小数，这使得每次切分都会有一个子组，那么总共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为O(n^2);
平均情况
每一次切分选择的基准数字不是大值和小值，也不是中值，这种情况我们也可以用数学归纳法证明，快速排序的时间复杂度为O(nlogn)

稳定性

不稳定