选择排序

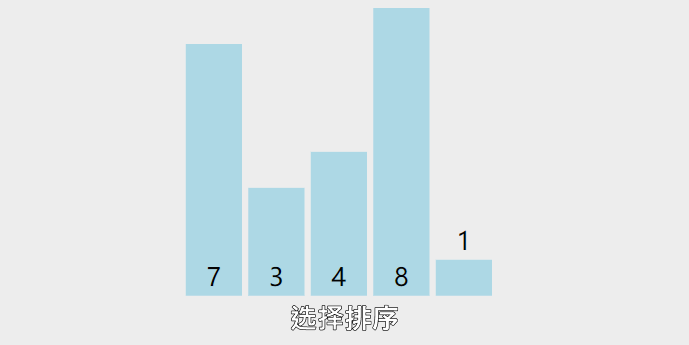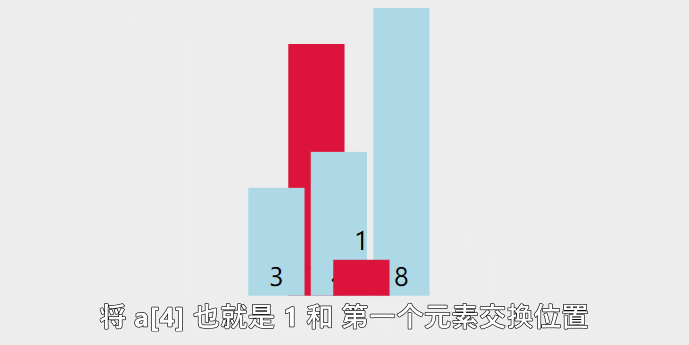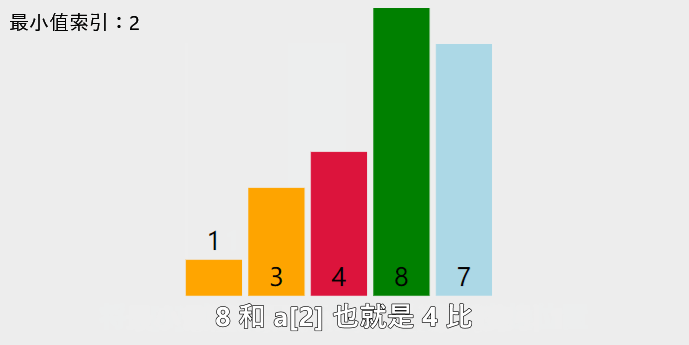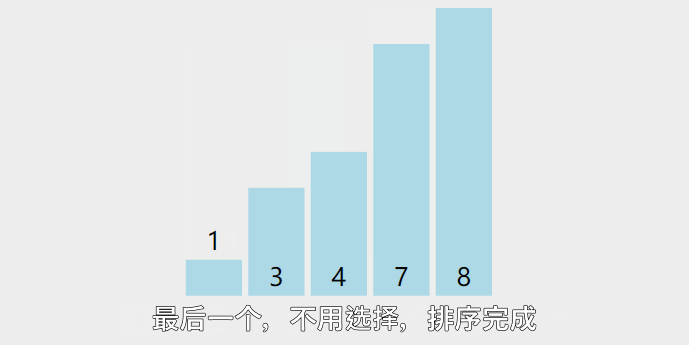
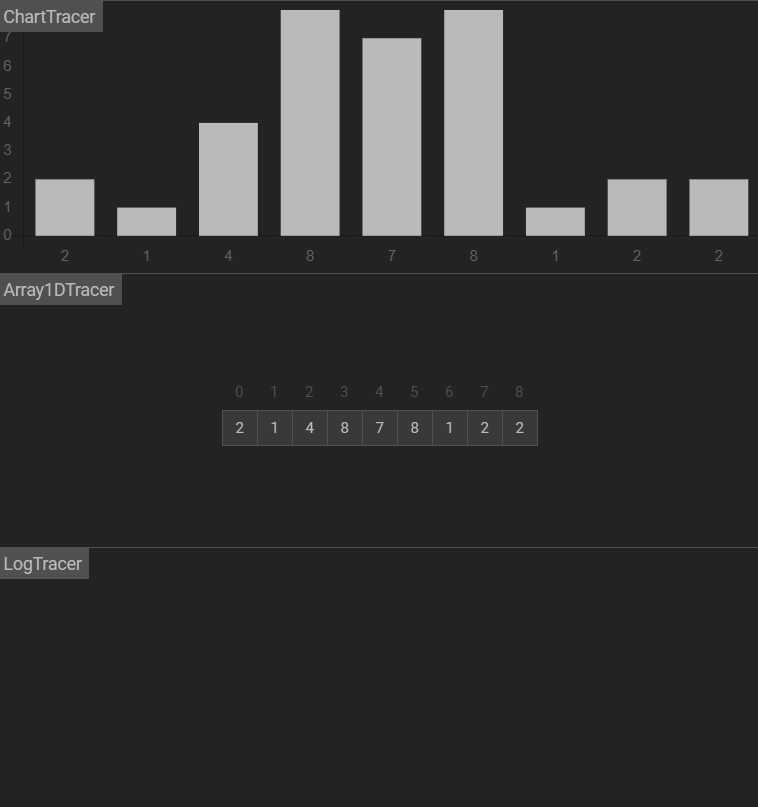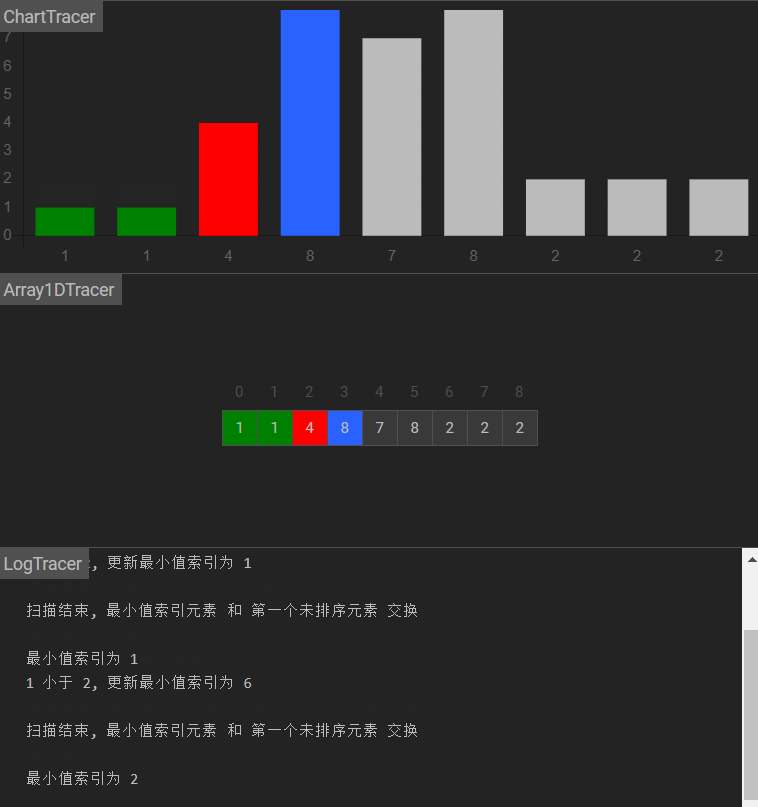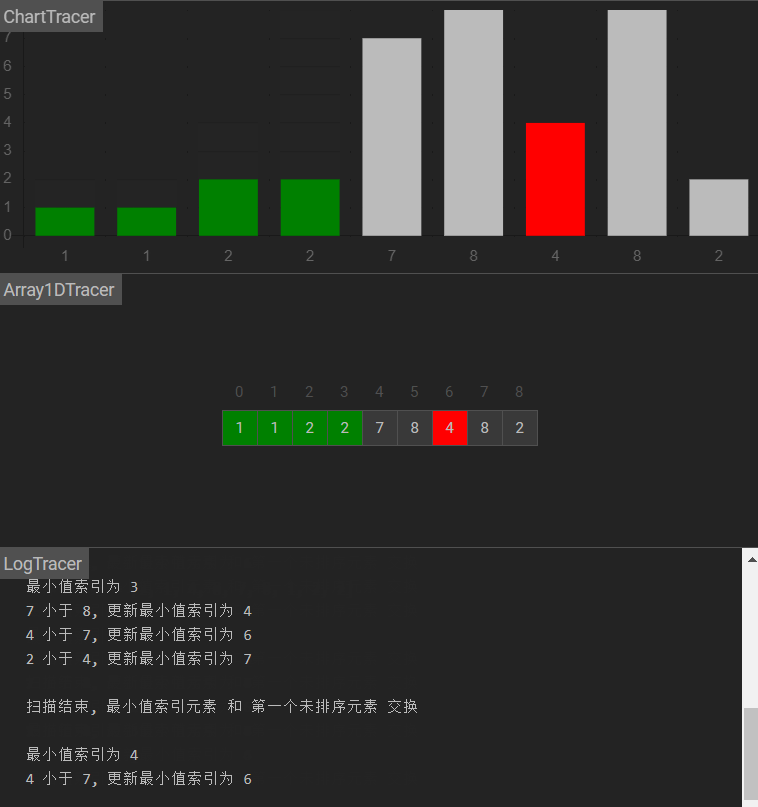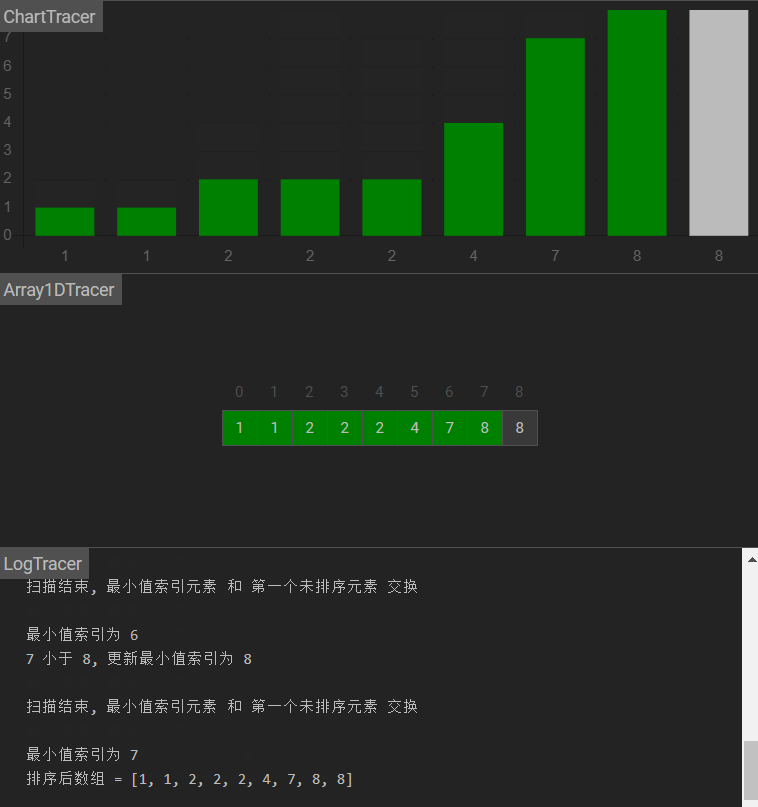
图示

原理

Code

1. 每一轮选择过程中，都假定该轮第一个索引处的元素是最小值
2. 和该轮其他值依次进行比较，如果其他值比先前假设的最小值还小，则更新最小值的索引
3. 经过一轮选择后，如果最小值索引和初始的最小值索引不一致，则交换他们的位置

如：7 3 4 8 1 2 5 9 6 0
10个数要选9轮，n个数选n-1轮
每选一轮，减少一个数参与选择
每轮m个数参与选择，要比较m-1次
外层循环控制选择的轮数
内层循环控制该轮选择要比较的次数

实现

java

public static void _从左往右选小数放到该轮首部(Comparable a[]){

        for (int i = 0; i < a.length - 1; i++) { //需要 元素个数-1 轮选择

            //假设最小值索引为0
            int _最小值索引 = i;

            //从 该轮的第二个元素 开始比较到最后一个元素
            for (int j = i+1; j <= a.length-1; j++) {
                if(_是否小于(a[j],a[_最小值索引])){
                    _最小值索引 = j;
                }
            }
            //将选择到的最小值，和该轮首部元素交换位置
            if(_最小值索引 != i){
                _交换(a, _最小值索引,i);
            }
        }
    }

性能

如6个数： [6,5,4,3,2,1]

需要比较的次数

Code

第一轮需要比较5次

第二轮需要比较4次

...

第五轮需要比较1次

需要交换的次数

Code

第一轮需要交换1次

第二轮需要交换1次

...

第五轮需要交换1次

N个数需要比较总次数：（N-1）+（N-2）+（N-3）+ … + 2 + 1 = ((N-1)+1) * (N-1)/2=N^2/2 - N/2

N个数需要交换总次数：（N-1）

总的执行次数为：N^2/2 - N/2 +（N-1）=N^2/2 + N/2-1

根据大O记法，时间复杂度为 O(N^2)

稳定性

不稳定