插入排序 | Juchia

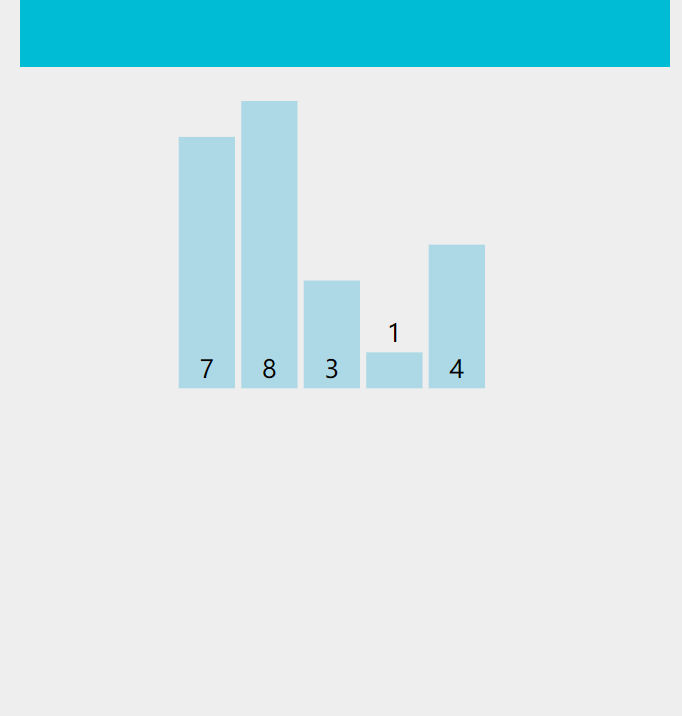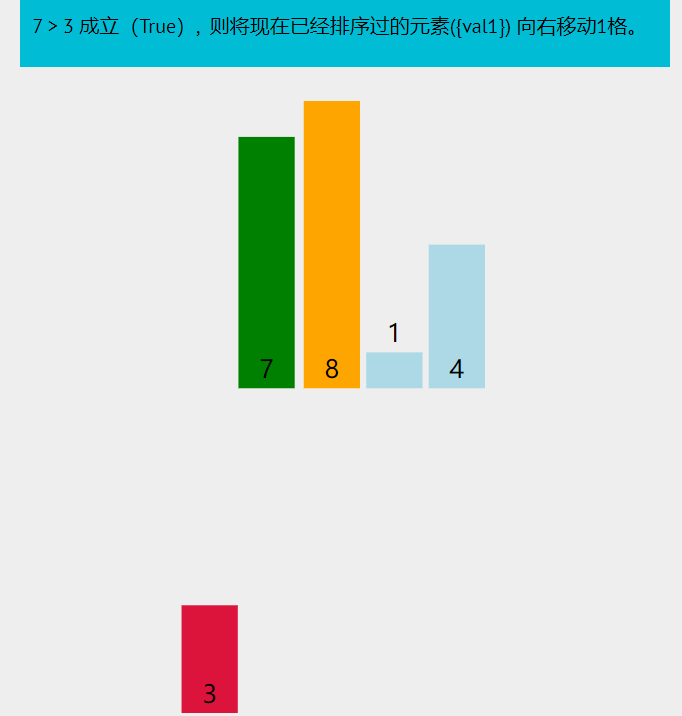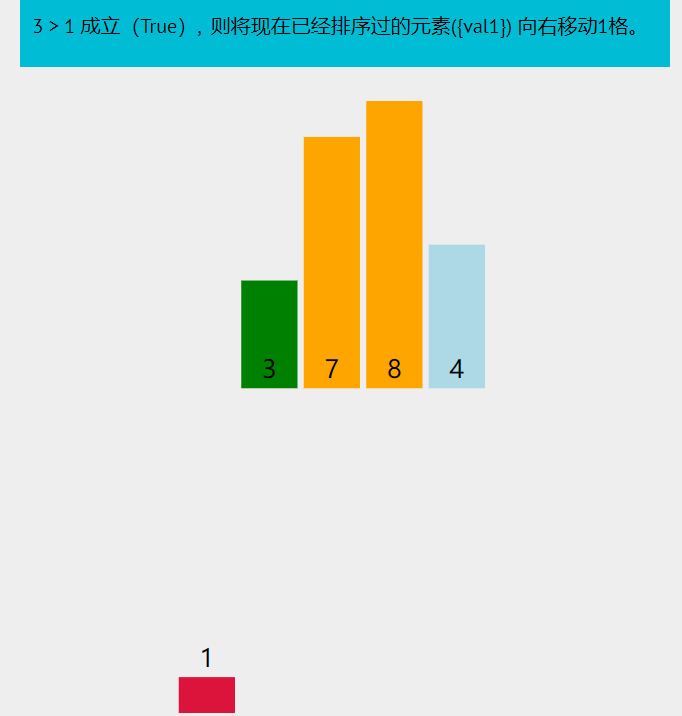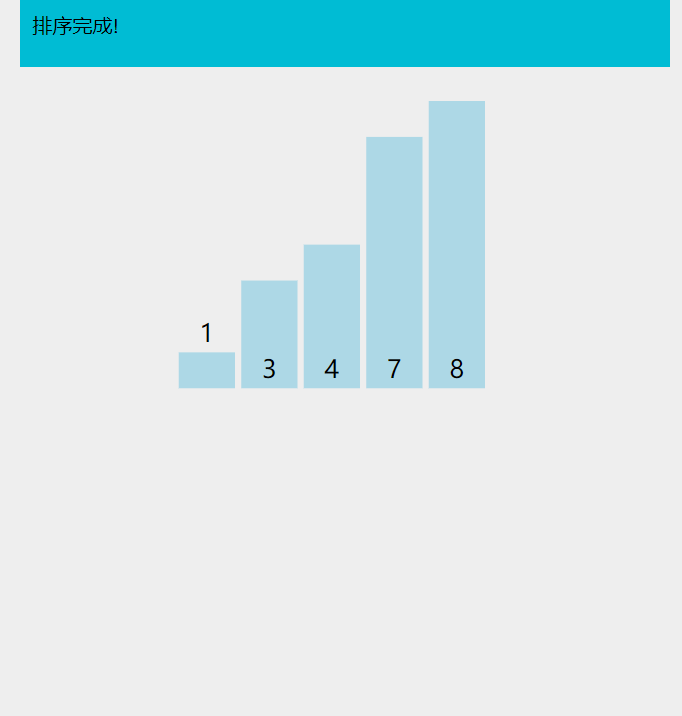
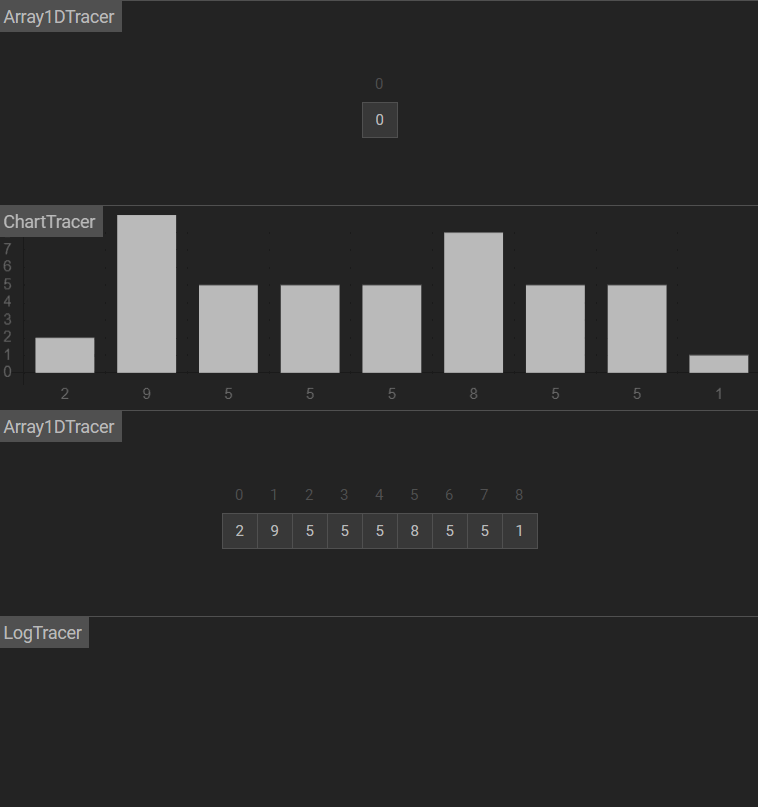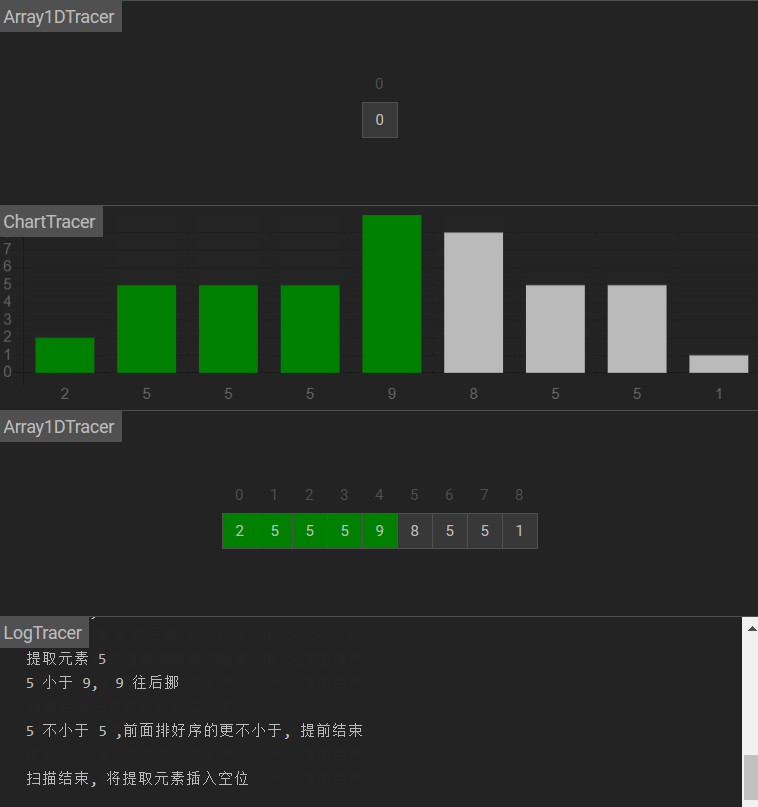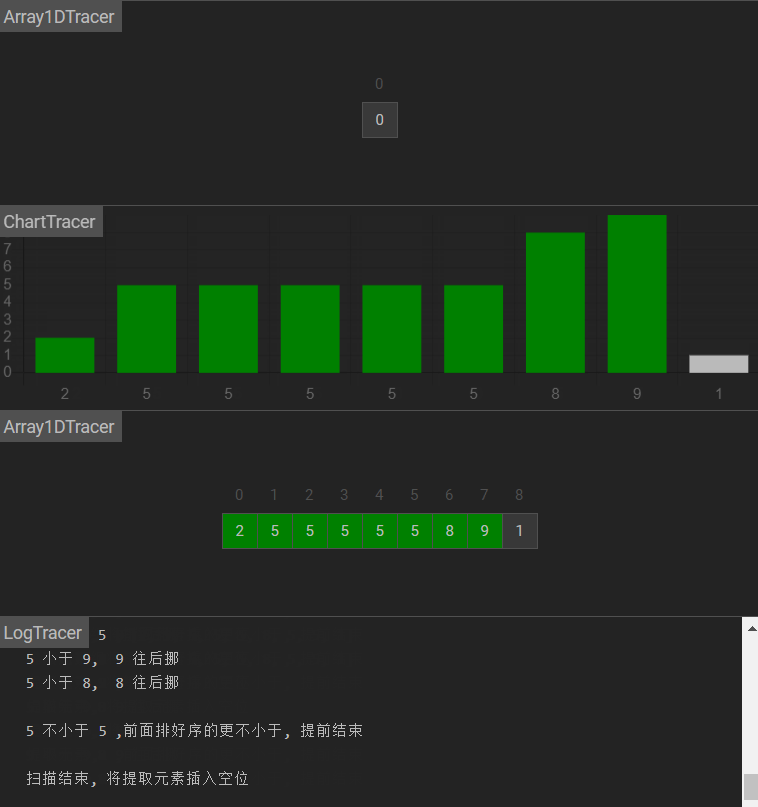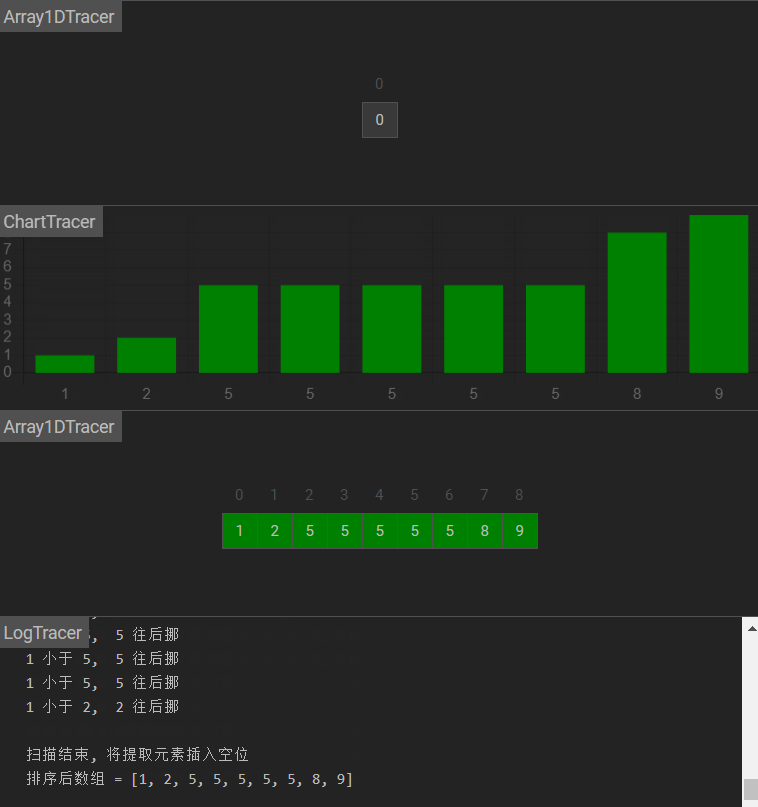
图示

原理

Code

1
2
3

1.把所有的元素分为两组，已经排序的和未排序的
2.每次从未排序的元素中“提取”第一个元素，依次逆序和已排序的元素进行比较
3.每比较一次，如果提取的元素比被比较的元素大，那么将被比较的元素往右挪一个位置，否则将提取的元素插到这个被比较元素后

实现

java

private static void _将已排好序的放左边_比提取元素大的往右挪一个位置(Comparable a[]){

        for (int i = 1; i < a.length ; i++) {

            // 从第二个元素开始提取, 因为第一个元素只有一个元素,说明它已经排好序了
            Comparable _提取元素 = a[i];

            int _将要插入的位置 = i;

            //_提取元素依次和前面已经排好序的元素比较
            for (int j = i-1; j >= 0; j--) {

                if(_是否小于(_提取元素,a[j])){ //如果提取的元素小于这个数,将这个数往右挪一个位置,并记录提取的元素将要插入的位置
                    _交换(a, j,j+1);
                    _将要插入的位置 = j;
                }else { //否则前面的数都比提取的这个数小, 没必要找了
                    break;
                }

            }

            if(_将要插入的位置!=i){
                a[_将要插入的位置] = _提取元素;
            }

        }
    }

性能

如6个数： [6,5,4,3,2,1]

需要比较的次数

Code

第一轮需要比较次

第二轮需要比较2次

...

第五轮需要比较5次

同理需要交换的次数

Code

第一轮需要交换1次

第二轮需要交换2次

...

第五轮需要交换5次

N个数需要比较总次数：1 + 2 + … + （N-3）+（N-2）+（N-1） = ((N-1)+1) * (N-1)/2 = N^2/2 - N/2

N个数需要交换总次数：1 + 2 + … + （N-3）+（N-2）+（N-1） = ((N-1)+1) * (N-1)/2 = N^2/2 - N/2

总的执行次数为：N^2/2 - N/2 + N^2/2 - N/2 = N^2-N

根据大O记法，时间复杂度为 O(N^2)

稳定性

稳定